3D Shearing

We can denote shearing with ‘SH_x,’ ‘SH_y,’ and ‘SH_z.’ These ‘SH_x,’ ‘SH_y,’ ‘SH_z’ are called “Shearing factor.”

The basic difference between 2D and 3D Shearing is that the 3D plane also includes the z-axis.

We can perform shearing on the object by following three ways-

• Shearing along the x-axis: In this, we can store the x coordinate and only change the y and z coordinate.

We can represent shearing along x-axis by the following equation-

x₁ = x₀

y₁ = y₀ + SH_y. x₀

z₁ = z₀ + SH_z. x₀

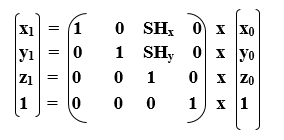
3D Shearing Matrix:

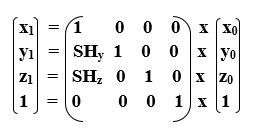
• Shearing along the y-axis: In this, we can store the y coordinate and only change the x and z coordinate.

We can represent shearing along with y-axis by the following equation-

x₁ = x₀ + SH_x. y₀

y₁ = y₀

z₁ = z₀ + SH_z. y₀

3D Shearing Matrix:

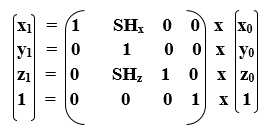
• Shearing along with z-axis: In this, we can store the z coordinate and only change the x and y coordinate.

We can represent shearing along with z-axis by the following equation-

x₁ = x₀ + SH_x. z₀

y₁ = y₀ + SH_y. Z_­0

z₁ = z₀

3D Shearing Matrix: