Association Rule Learning Algorithm
Introduction to Association Rule Learning
Association rule learning extracts alliances among the datapoints in a huge dataset. It incorporates the concept of data mining, which helps in finding useful commercial associations or regularities between the variables. It is presently in use in the sales industry to predict if the person will buy item A based on his previous purchase B. It is widely used by the corporations to discover the relation between the articles that are often purchased by the customer.
It is based on if/then statements. It is basically used to disclose the relations between the datapoints or the entities that are often used together. A set of transactions is given below, such that we will predict the occurrence of an item based on some other items manifestation.
| Transaction_Id | Items |
| (a) | Chocolate, Chips, |
| (b) | Chocolate, Shoes, Purse, Pastry |
| (c) | Chips, Shoes, Purse, Eggs |
| (d) | Chocolate, Chips, Shoes, Purse |
| (e) | Chocolate, Chips, Shoes, Eggs |
To demonstrate more about the concept of association rule learning, we are considering an example of the supermarket domain. The items contained in the set are Chocolate, Chips, Pastry, Shoe and Purse, i.e., I = {Chocolate, Chips, Pastry, Shoe, Purse, Eggs}, and the entries in the table depicts 1 for the occurrence of an item in the corresponding transaction and 0 if not present.
Before moving ahead, let's look into some important terms:
- Support Count (?): It is the rate of occurrence of an itemset.
Therefore, ?({Chocolate, Chips, Shoes})=2
- Frequent Itemset: The support of an itemset that is more than or equal to the minsup threshold.
- Association Rule: It involves an expression which is in the form of P–›Q, such that P and Q are the elements.
Here, {Chocolate, Chips}–›{Shoes} states that if a customer purchases Chocolate and Chips, then he also buy Shoes.
Rule Evaluation Metrics
- Support: Support is an evidence of how often the itemset occurs in the dataset. It is the fraction of transactions that encompass both P and Q.
Example:{Chocolate, Chips}–›{Shoes}
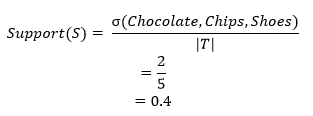
- Confidence:It is an indication of how frequent the rule is found to be true. It measures how frequent items in Q appear in transactions that consist of P.
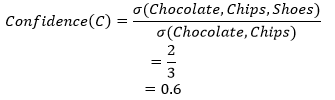
- Lift:It is the probability of the itemset Q being purchased when item P is bought considering the popularity of Q.
Goals of Association Rule Mining
Following are some goals to find some rules when association rule mining is applied on a given set of transactions T:
- Support that is equal to or greater than min_support.
- Confidence that is equal to or greater than min_confidence.
Applications of Association Rule Mining
- Market-based analysis
- Medical diagnosis
- Protein sequences
- Census data
- CRM of credit card business, etc.
Association Rule Mining Algorithms
Following are the association rule mining algorithms give below:
- Apriori Algorithm
Apriori algorithm is one of the most powerful algorithms used for data extraction. It mainly mines frequent itemset and appropriate association rules. It is implemented on the dataset that comprises a set of transactions. It is vital for market basket analysis to examine which product is going to be purchased next by the customer. It is a bottom-up approach. It will help in increasing the market sale. Other than the market basket, it is also seen in the field of healthcare.
Advantages of Apriori Algorithm
- Easy implementation on large itemset.
- Easy to understand.
Disadvantages of Apriori Algorithm
Finding large no of candidate rules as well as evaluating support tends out to be computationally expensive.
- Eclat Algorithm
It is the most popular and powerful scheme for association rule mining. The full form of Eclat is Equivalence Class Clustering and bottom-up Lattice Traversal. It is better than the Apriori algorithm in terms of efficiency and scalability. The Apriori algorithm works the same as the breadth-first search, whereas the Eclat algorithm works as a depth-first search, which in turn makes it run faster than the Apriori algorithm. The set intersections are used to calculate the support of the candidates items while avoiding the generation of subdivisions that are not present in the prefix tree.