Banker’s Algorithm in Operating System
What is Banker’s Algorithm?
Bankers algorithm is an algorithm which is used for deadlock avoidance and resource allocation. It was established by Edsger Dijkstra. The reason behind the name ‘banker’s algorithm’ is that it is mostly used in banking systems. Banker’s algorithm helps to identify whether a loan should be provided or not.
Characteristics of Banker’s Algorithm
The characteristics of Banker’s algorithm are:
- If a process demands the resources, then it has to wait.
- Banker’s algorithm consists of advanced features for maximum resource allocation.
- In the banker’s algorithm, various resources are maintained that fulfill the needs of at least one client.
- In the system, we have limited resources.
- In the banker’s algorithm, if the process gets all the needed resources, then it is must to return the resources in a restricted period.
Disadvantages of Banker’s Algorithm
The disadvantages of banker’s algorithm are:
- During processing, it does not permit a process to change its maximum need.
- All the processes should know in advance about the maximum resource needs.
- Banker’s algorithm permits the requests to be provided in constrained time, but for one year which is a fixed period.
Data Structures used to implement the Banker’s Algorithm
There are four types of data structures used to implement Banker’s algorithm:
- Available
- Max
- Allocation
- Need
1. Available
- Available is a one-dimensional array. The size of the array is ‘m’ which is used to determine the number of available resources of each kind.
- Available[j] = k indicates that we have ‘k’ instances of ‘Rj’ resource type.
2. Max
- Max is a two-dimensional array. The size of the array is ‘n*m’. The max data structure is used to determine the maximum number of resources that each process requests.
- Max[i, j] = k indicates that ‘Pi’ can demand or request maximum ‘k’ instances of ‘Rj’ resource type.
3. Allocation
- Allocation is a two-dimensional array, and the size of the array is ‘n*m’, which is used to define the number of resources of each kind presently assigned to each process.
- Allocation[i, j] = k indicates that currently process ‘Pi’ is assigned ‘k’ instances of ‘Rj’ resource type.
4. Need
- Need is a two-dimensional array. The size of the array is ‘n*m’. Need is used to define the remaining resources which are required for each process.
- Need [i, j] = k indicates that for the execution of ‘Pi’ process, presently ‘k’ instances of resource type ‘Rj’ are required.
Banker’s algorithm comprises of two algorithms:
- Safety algorithm
- Resource request algorithm
1. Safety algorithm
The safety algorithm is used to check the system state means whether the system is in a safe state or not.
The safety algorithm contains the following steps:

2. Resource Request Algorithm
Let Requesti is the request array for the process ‘Pi’. Requesti [j] = k means ‘Pi’ process needs k instances of Rj resource type. At the time when a process Pi demands resources, then we follow the below steps.

Example of Banker’s Algorithm
Consider the following snapshot of a system:
| Processes | Allocation A B C | Max A B C | Available A B C |
| P0 | 1 1 2 | 4 3 3 | 2 1 0 |
| P1 | 2 1 2 | 3 2 2 | |
| P2 | 4 0 1 | 9 0 2 | |
| P3 | 0 2 0 | 7 5 3 | |
| P4 | 1 1 2 | 1 1 2 |
- calculate the content of the need matrix?
- Is the system in a safe state?
- Determine the total amount of resources of each type?
Solution:
1. Content of the need matrix can be calculated by using the below formula
Need = Max – Allocation
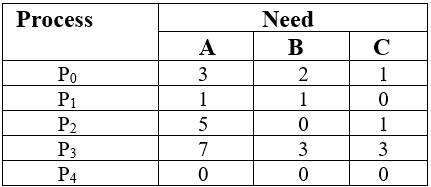
??
2. Now, we check for a safe state
Safe sequence:
- For process P0, Need = (3, 2, 1) and
Available = (2, 1, 0)
Need ? Available = False
So, the system will move for the next process.
2. For Process P1, Need = (1, 1, 0)
Available = (2, 1, 0)
Need ? Available = True
Request of P1 is granted.
? Available = Available +Allocation
= (2, 1, 0) + (2, 1, 2)
= (4, 2, 2) (New Available)
3. For Process P2, Need = (5, 0, 1)
Available = (4, 2, 2)
Need ? Available = False
So, the system will move to the next process.
4. For Process P3, Need = (7, 3, 3)
Available = (4, 2, 2)
Need ? Available = False
So, the system will move to the next process.
5. For Process P4, Need = (0, 0, 0)
Available = (4, 2, 2)
Need ? Available = True
Request of P4 is granted.
? Available = Available + Allocation
= (4, 2, 2) + (1, 1, 2)
= (5, 3, 4) now, (New Available)
6. Now again check for Process P2, Need = (5, 0, 1)
Available = (5, 3, 4)
Need ? Available = True
Request of P2 is granted.
? Available = Available + Allocation
= (5, 3, 4) + (4, 0, 1)
= (9, 3, 5) now, (New Available)
7. Now again check for Process P3, Need = (7, 3, 3)
Available = (9, 3, 5)
Need ? Available = True
Request of P3 is granted.
? Available = Available +Allocation
= (9, 3, 5) + (0, 2, 0) = (9, 5, 5)
8. Now again check for Process P0, = Need (3, 2, 1)
= Available (9, 5, 5)
Need ? Available = True
So, the request will be granted to P0.
Safe sequence: < P1, P4, P2, P3, P0>
The system allocates all the needed resources to each process. So, we can say that system is in a safe state.
3. The total amount of resources = sum of columns of allocation + Available
= [8 5 7] + [2 1 0] = [10 6 7]
Related Posts:
- File Access Methods in Operating System
- Directory Structure in Operating System
- File Allocation Methods in Operating System
- Producer-Consumer Problem in OS
- Partitioning Algorithms
- Virtual Memory in Operating System
- Deadlock Prevention in Operating System
- SCAN Disk Scheduling Algorithm
- Disk Scheduling Algorithms
- Look Disk Scheduling
- Difference between Multi-programming and Multitasking
- Lock Variable Mechanism | Operating System