Bresenham’s Circle Drawing Algorithm in Computer Graphics

Bresenham’s algorithm is also used for circle drawing. It is known as Bresenham’s circle drawing algorithm. It helps us to draw a circle. The circle generation is more complicated than drawing a line. In this algorithm, we will select the closest pixel position to complete the arc. We cannot represent the continuous arc in the raster display system. The different part of this algorithm is that we only use arithmetic integer. We can perform the calculation faster than other algorithms. 

Let us assume we have a point p (x, y) on the boundary of the circle and with r radius satisfying the equation f_c (x, y) = 0

As we know the equation of the circle is –

f_c (x, y) = x² + y² = r²

If

     f_c (x, y) < 0

then

      The point is inside the circle boundary.

If

     f_c (x, y) = 0

then

      The point is on the circle boundary.

If

     f_c (x, y) > 0

then

      The point is outside the circle boundary.

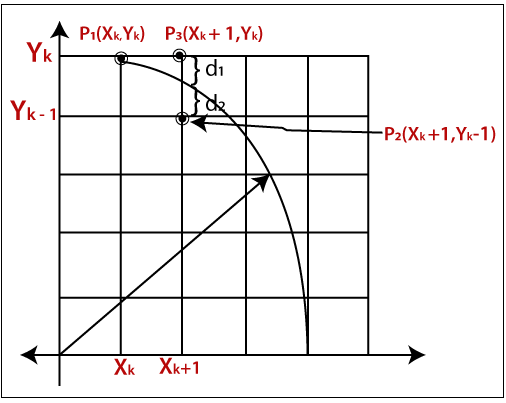
We assume,

The distance between point P₃ and circle boundary = d₁

The distance between point P₂ and circle boundary = d₂

Now, if we select point P₃ then circle equation will be-

d₁ = (x_k +1)² + (y_k)² – r²            {Value is +ve, because the point is outside the circle}

if we select point P₂ then circle equation will be-

d₂ = (x_k +1)² + (y_k -1)² – r²                {Value is -ve, because the point is inside the circle} 

Now, we will calculate the decision parameter (d_k) = d₁ + d₂

d_k =(x_k +1)² + (y_k)² – r² + d₂ + (x_k +1)² + (y_k -1)² – r²

    = 2(x_k +1)² + (y_k)²+ (y_k -1)² – 2r²                  …………………… (1)

If  

      d_k < 0

then

       Point P₃ is closer to circle boundary, and the final coordinates are-

(x_{k +1}, y_k) = (x_k +1, y_k)

If  

      d_k >= 0

then

       Point P₂ is closer to circle boundary, and the final coordinates are-

(x_{k +1}, y_k) = (x_k +1, y_k -1)

Now, we will find the next decision parameter (d_k+1)

(d_k+1) = 2(x_k+1 +1)² + (y_k+1)²+ (y_k+1 -1)² – 2r²               …………………… (2)

Now, we find the difference between decision parameter equation (2) - equation (1) (d_k+1) – (d_k) = 2(x_k+1+1)² + (y_k+1)²+ (y_k+1 –1)² – 2r² – 2(x_k +1)² + (y_k)²+ (y_k– 1)² – 2r²        (d_k+1) = d_k + 4x_k + 2(y_k+1²– y_k²) – (y_k+1 – y_k) + 6

Now, we check two conditions for decision parameter-

Condition 1: If

                          d_k < 0

                      then

                           y_k+1 = y_k   (We select point P₃)

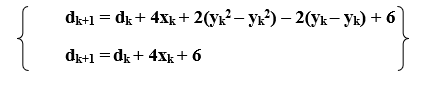
Condition 2: If

                          d_k >= 0

                      then

                           y_k+1 = y_k-1       (We select point P₃)

Now, we calculate initial decision parameter (d₀)

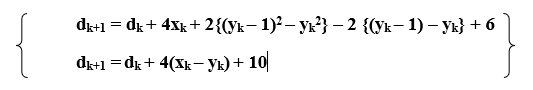
d₀ = d₁ + d₂

d₀ = {1² +r²– r²} + {1² +(r – 1)² – r²}               

d₀ =   3 – 2r                                                                      

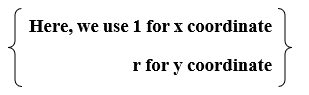
Algorithm of Bresenham’s Circle Drawing

Step 1: Start.

Step 2: First, we allot the starting coordinates (x₁, y₁) as follows-

             x₁ = 0

             y₁ =r

Step 3: Now, we calculate the initial decision parameter d₀ -

                                                                 d₀ = 3 – 2 x r

Step 4: Assume,the initial coordinates are (x_k, y_k)

                  The next coordinates will be (x_k+1, y_k+1) 

Now, we will find the next point of the first octant according to the value of the decision parameter (d_k).      

Step 5: Now, we follow two cases-

Case 1: If

                  d_k < 0

         then

                  x_k+1 =x_k + 1

                  y_k+1 =y_k

                  d_k+1 = d_k + 4x_k+1 + 6

Case 2: If

                  d_k >= 0

         then

                  x_k+1 =x_k + 1

                  y_k+1 =y_k –1

                  d_k+1 = d_k + 4(x_k+1 – y_k+1)+ 10

Step 6: If the center coordinates (x₁, y₁) is not at the origin (0, 0), then we will draw the points as follow-

X coordinate = x_c + x₁

y coordinate = y_c + y₁              {x_c andy_c representsthe current value of x and y coordinate}

Step 7: We repeat step 5 and 6 until we get x>=y.

Step 8: Stop.

Example: The radius of a circle is 8, and center point coordinates are (0, 0). Apply bresenham’s circle drawing algorithm to plot all points of the circle.

Solution:  

Step 1: The given stating points of the circle (x_1, y₁) = (0, 0)

              Radius of the circle (r) = 8

Step 2: Now, we will assign the starting point (x_1, y₁) as follows-

             x₁ = 0

             y₁ = r (radius) = 8     

Step 3: Now, we will calculate the initial decision parameter (d₀)

                 d₀ = 3 – 2 x r

          d₀ = 3 – 2 x 8

          d₀ = -13

Step 4:  The value of initial parameter d₀ < 0. So, case 1 is satisfied.

Thus,

                   x_k+1 =x_k + 1 = 0 + 1 = 1

           y_k+1 =y_k = 8

           d_k+1 = d_k + 4x_k+1 + 6 = -13 + (4 x 1) + 6 = -3

Step 5: The center coordinates are already (0, 0) so we will move to next step.

Step 6: Follow step 4 until we get x >= y.

Table for all points of octant 1:

dk	dk+1	(xk+1,yk+1)
		(0, 8)
­-13	-3	(1, 8)
-3	11	(2, 8)
11	5	(3, 7)
5	7	(4, 6)
7		(5, 5)

Now, we will calculate the coordinates of the octant 2 by swapping the x and y coordinates.

Coordinates of Octant 1	Coordinates of Octant 2
(0, 8)	(5, 5)
(1, 8)	(6, 4)
(2, 8)	(7, 3)
(3, 7)	(8, 2)
(4, 6)	(8, 1)
(5, 5)	(8, 0)

Thus, we will calculate all points of the circle with respect to octant 1.  

Quadrant 1 (x, y)	Quadrant 2 (-x, y)	Quadrant 3 (-x, -y)	Quadrant 4 (x, -y)
(0, 8)	(0, 8)	(0, -8)	(0, -8)
(1, 8)	(-1, 8)	(-1, -8)	(1, -8)
(2, 8)	(-2, 8)	(-2, -8)	(2, -8)
(3, 7)	(-3, 7)	(-3, -7)	(3, -7)
(4, 6)	(-4, 6)	(-4, -6)	(4, -6)
(5, 5)	(-5, 5)	(-5, -5)	(5, -5)
(6, 4)	(-6, 4)	(-6, -4)	(6, -4)
(7, 3)	(-7, 3)	(-7, -3)	(7, -3)
(8, 2)	(-8, 2)	(-8, -2)	(8, -2)
(8, 1)	(-8, 1)	(-8, -1)	(8, -1)
(8, 0)	(-8, 0)	(-8, 0)	(8, 0)

Advantages of Bresenham’s Circle Drawing Algorithm

• It is simple and easy to implement.
• The algorithm is based on simple equation x² + y² = r².

Disadvantages of Bresenham’s Circle Drawing Algorithm

• The plotted points are less accurate than the midpoint circle drawing.
• It is not so good for complex images and high graphics images.

Related Posts:

• Bresenham’s Line Drawing Algorithm in Computer Graphics
• Line Drawing Algorithm in Computer Graphics
• Mid-Point Line Drawing Algorithm in Computer Graphics
• Midpoint Circle Drawing Algorithm in Computer Graphics
• DDA line Drawing Algorithm in Computer Graphics
• Line Clipping in Computer Graphics
• Animation in Computer Graphics
• Image Representation in Computer Graphics
• Pointing and Positioning Technique Computer Graphics
• Scan Conversion of a Circle Computer Graphics