Closure Properties of Regular Languages -Automata
Closure Properties of Regular Languages
We use the term “Closure” when we talk about sets of things. If we have two regular languages L1 and L2, and L is obtained by applying certain operations on L1, L2 then L is also regular.
Consider an Example: Let us take a set of candy. Each member of the set contains an individual pieces of candy. Suppose we have taken a candy from the set candy and dropped it on the clean ground, now what happen? We can still eat it, so it is still candy. The set candy is closed under the operation called “drop”.
Closure Properties used in Regular Languages are as follows:
- Union
- Concatenation
- Complementation
- Intersection
- Reversal
- Difference
- Homomorphism
- Inverse Homomorphism
Union
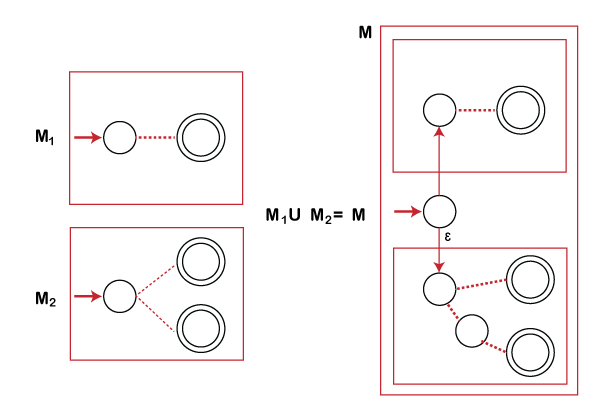
Theorem: If L1 and L2 are regular languages, then their union L1 U L2 is also a regular language.
Proof: Let M1 and M2 are two finite automata accepting L1 and L2 regular language. If we want to prove that the union of L1 U L2 is also a regular language then we can perform following steps:
- Create a new initial state.
- Make ?-transitions from new state to each of the original state of M1 and M2.
Concatenation
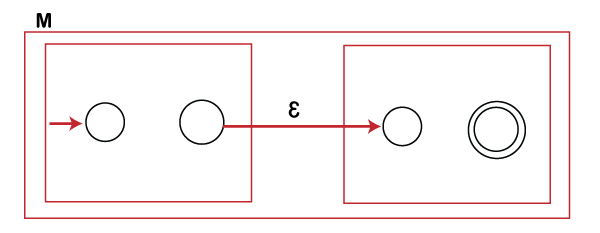
Theorem: The Concatenation operation of two regular languages is also regular.
Proof: Let M1 and M2 are two finite automata, and L1, L2 are the languages accepted by the M1 and M2 respectively. We want to prove that L1L2 = L i.e. their concatenation results in regular language. Let M is finite automata combining M1 and M2.
Closure or Star
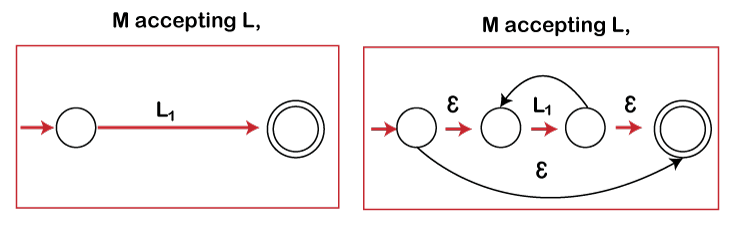
In this, the theorem depicts that the closure or star of any regular languages is also regular.
Proof: Let L1 is regular language and we want to prove that L1* is also regular language, the proof is given below:
- Create a new initial state connect it to original state start with ?-transition.
- Create a new final. Connect the original final state to it with ?-transitions. The original final state will be non-final state.
- Connect the new initial state and new final state with a pair of ?-transitions.
Let L1 is accepted by finite automata M. Now we have to prove that M also accepts L1*.
Complementation
Theorem: The complement of two regular language is also regular.
Proof: Let M be a deterministic finite automata accepting L, then we can write L= L(M), then L’ = L(M1). The DFA M1 is like M but the accepting states of M are now non-accepting states of M1 and vice versa.
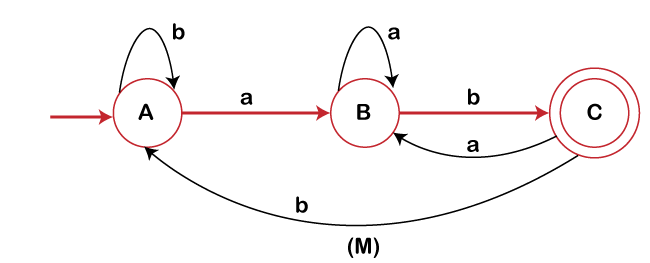
The complement of above langages is:
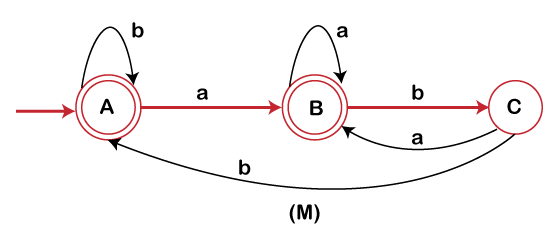
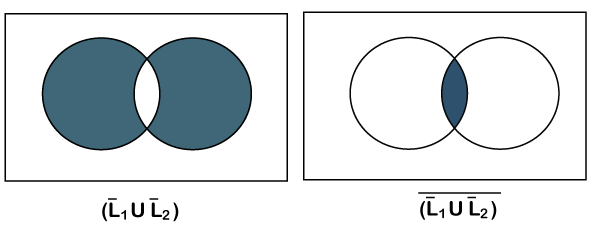
Intersection:
Theorem: The set of regular languages are closed under intersection.
Proof: Let L1 and L2 are regular language and we want to prove that the intersection of L1 ? L2 is also a regular language. We can obtain the intersection of language L1 ? L2 by De Morgen’s Law.
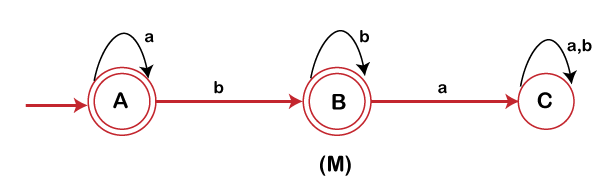
Reversal
Theorem: The set of regular languages are closed under reversal.
Proof: Let M be a deterministic finite automata accepting L, from M we will construct M’ such that states of M and M’ are same. Make final state of M as initial state of M’ and initial state of M as accepting state of M’. The direction of edges in M’ is reversed. It means that the string written backward i.e.
Reversal of abbc is cbba
The reverse of above language is shown below:
Difference
Theorem: If L1 and L2 are regular languages then L1-L2 is also regular
Proof:
L1-L2 = L1 ? L2’
As we know L2 is regular then its complement L2 is also regular and L1 ? L2’ is also regular, so it proves that L1-L2 is also regular.
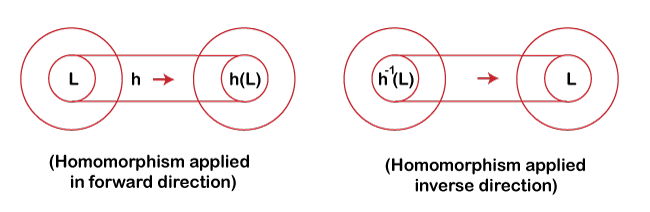
Homomorphism
The Homomorphism theorem depicts that a single letter is replaced with a string. If h is a homomorphism on alphabet ? and w = a1a2……….an is a string of symbols in ?, then
h(w) = h(a1)h(a2)…………………..h(an)
If L is a language over alphabet ?then itshomomorphism h is defined as:
h(L) = {h(w) : w ? L }
Inverse Homomorphism
The inverse homomorphism theorem states that if h is a homomorphism from alphabet ? to alphabet A and L is a regular language on A then h’(L) is also a regular language.