Conversion from Moore Machine to Mealy Machine
Conversion from Moore Machine to Mealy Machine
Moore Machine
The output of Moore machine depends only on the present state. In this, if machine has N number of states, then it will require N-flip-flops, where M is the smallest number such that N<=2M. In this, if the input string is of length n, then the output string will be of length n+1.
Mealy Machine
In Mealy machine value of output function depends on the current state q (t) and current input i (t). In this, if machine has N number of states then it will require N-flip-flops, where M is the smallest number such that N<=2M. In mealy machine, if the input string of length n, then the output string will be of length n.
Method for conversion of Moore machine to Mealy machine
Theorem:
If M = (Q, q0, ?, O, ?, ?) is a Moore machine, then there exists a mealy machine M’ = (Q, q0, ?, O, ?, ?') equivalent to M.
Proof:
If M’ = (Q, q0, ?, O, ?, ?) is a Mealy machine, we can define ?’ to be ? (? (q, a)) for all state q and input symbols a. The M’ will be equivalent to M since they enter the same sequence of states on the same input, and with each transition M’ has the same output that M associate with the state entered.
There are two methods for converting a Moore Machine to Mealy Machine
- Converting a Moore Machine to Mealy Machine using transition diagram
- Converting a Moore Machine to Mealy Machine using transition table
Converting a Moore Machine to Mealy Machine using transition diagram
In this method, we convert the Moore machineto Mealy Machine by using transition diagram of Moore machine.
Following steps are used to convert Moore machine to Mealy Machine:
Step1: Consider any state in Moore machine q0.
Step2: Check the output corresponding to this state, which is a.
Step3: Check how many edges are entering into this state. As in q0 two edges, labelled 0 and 1 are entering.
Step4: Remove the output of q0 from inside the state and put it on the entering edges like 0/a and 1/a. This means that we have output a on the incoming edges before they enter state q0.
Step5: Follow the above steps for every state q0, q1…………………qn of Moore machine, which turns Moore machine M into an equivalent mealy machine M’. It will give same output string corresponding to all input strings.
Example
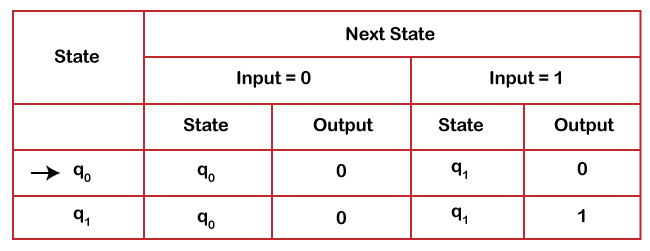
Convert the following Moore machine to mealy machine using transition diagram.
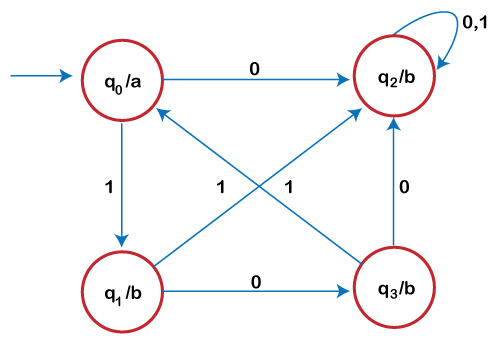
Solution:
In this method, we convert the Moore machine to mealy machine by using the transition diagram to Moore machine.
The transition table of given Moore machine is as follows:
| Current State (Q) | Input 0 | Input 1 | Output(?) |
| q0 | q2 | q1 | a |
| q1 | q3 | q2 | b |
| q2 | q2 | q2 | b |
| q3 | q2 | q0 | b |
The equivalent mealy machine can be obtained by finding the output of following states:
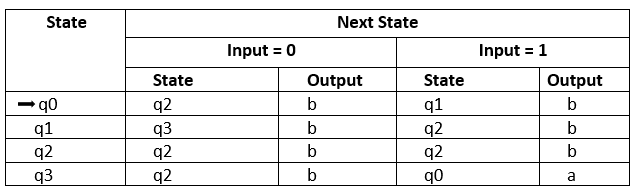
Firstly, we find the output of state q0 for input 0 and 1
?' (q0, 0) = ? (?(q0, 0))
= ? (q2)
= b
?' (q0, 1) = ? (?(q0, 1))
= ? (q1)
= b
The output for state q1 for input 0 and 1 is as follows:
?' (q1, 0) = ? (?(q1, 0))
= ? (q3)
= b
?' (q1, 1) = ? (?(q1, 1))
= ? (q2)
= b
The output for state q2 for input 0 and 1 is as follows:
?' (q2, 0) = ? (?(q2, 0))
= ? (q2)
= b
?' (q2, 1) = ? (?(q2, 1))
= ? (q2)
= b
The output for state q3 for input 0 and 1 is as follows:
?' (q3, 0) = ? (?(q3, 0))
= ? (q2)
= b
?' (q3, 1) = ? (?(q3, 1))
= ? (q0)
= a
The equivalent transition table for the Mealy machine is shown below:
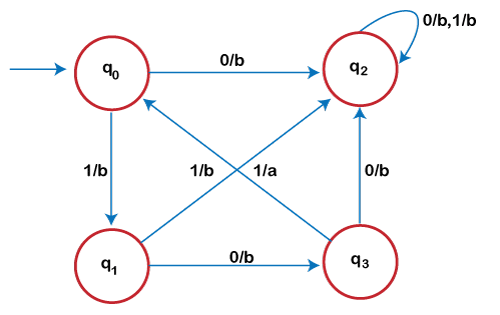
The equivalent mealy machine for given Moore machine is shown below:
Converting a Moore Machine to Mealy Machine using transition table
In this method, we convert the Moore machine to Mealy machine using transition table.
Example:
Convert the Moore machine represented by the below transition table to Mealy Machine.
| Current state (Q) | Input 0 | Input 1 | Output(?) |
| q0 | q0 | q1 | 0 |
| q1 | q0 | q2 | 0 |
| q2 | q0 | q2 | 1 |
The equivalent mealy machine can be obtained by finding the output of following states:
Firstly, we find the output of state q0 for input 0 and 1:
?' (q0, 0) = ? (?(q0, 0))
= ? (q0)
= 0
?' (q0, 1) = ? (?(q0, 1))
= ? (q1)
= 0
The output for state q1 for input 0 and 1:
?' (q1, 0) = ? (?(q1, 0))
= ? (q0)
= 0
?' (q1, 1) = ? (?(q1, 1))
= ? (q2)
= 1
Now we find the output for state q2 for input 0 and 1
?' (q2, 0) = ? (?(q2, 0))
= ? (q0)
= 0
?' (q2, 1) = ? (?(q2, 1))
= ? (q2)
= 1
The equivalent transition table for Mealy Machine is given below:
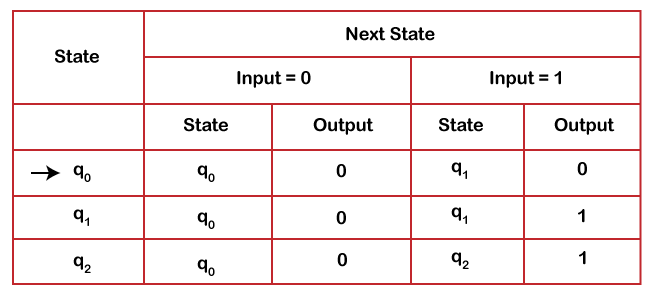
In above Mealy machine table, there are two identical transitions. The row for q1 and q2, both are same, which means, on state q1, q2 on input 0, the machine moves to same state q0. On input 1, from q1 and q2 the machine moves to same state q2. So, we will delete one row from these two rows. In above table q1 and q2 rows are identical so we will delete q2 from the transition table and replace q2 by q1 in other rows.
The final mealy machine is given below: