Data Flow Analysis in Compiler Design

Data Flow Analysis

All the optimization techniques we have learned earlier depend on data flow analysis. DFA is a technique used to know about how the data is flowing in any control-flow graph.

Example:

Forglobal common sub-expression elimination, we need to find the expression that computes the same value along with any available execution path of the program.

The Data-Flow Analysis Schema

In data flow analysis, a data flow value associates with every program point represents an abstraction for a set of all possible program states for that point.

The domain of this application is a set of possible data flow values.

IN[a]: The data flow value before the statement a.

OUT[a]: The data flow valueafter the statement a.

The main aim of the data flow problem is to find a set of constraints on the IN[a]'s and OUT[a]'s for statements a.

There are two sets of constraints: Transfer function and control-flow constraints.

Transfer Function

The semantic of the statement are the constraints for the data flow values before and after a statement.

For example, if variable x has the value y before executing any statement, say p = x. Then, after the statement's execution, the value for both x and p will be y.

The transfer function is the relationship between the data flow values before and after the assignment statement.

Transfer function comes in two ways:

• Forward propagation along with execution path
• Backward propagation up the execution path

Forward Propagation:

The following points should be considered:

• In forward propagation, the transfer function for any statement s will be represented by Fs.
• This transfer function takes the data flow values before the statement and produces the output or new data flow value after the statement.
• So the new data flow values after the statement will be OUT[s] = Fs (IN[s]).

Backward propagation:

The following points should be considered:

• Backward propagation is the converse of forward propagation.
• This transfer function converts a data flow value after the statement to a new data flow value before the statement.
• So the new data flow values will be IN[s] = Fs (OUT[s]).

Control-Flow Constraints

The second set of constraints is derived from the flow of control. If block B consists of statements S1, S2, ........, Sn, then the control flow value of Si will be equal to the control flow values into Si + 1. Which is:

IN [ Si +1 ] = OUT [ Si ], for all i = 1 , 2, .....,n – 1.

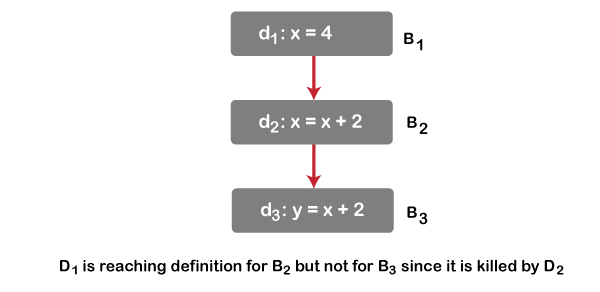
Reaching Definition

The most common and useful data flow scheme is Reaching Definition. A definition D reaches the point P along with path following D to P such that D is not killed along the path.

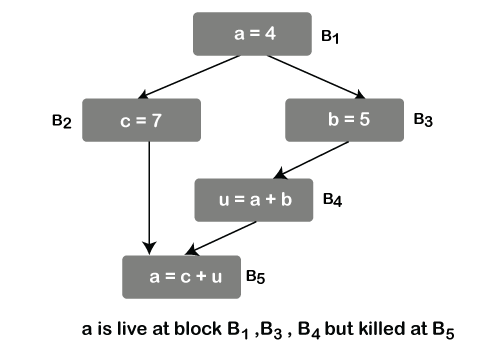
Live-Variable Analysis

Here we know about the value of a variable at point p is used from point p to the end. It means that the variable is live at point p; otherwise variable is dead at point p.

This is used for register allocation for basic blocks.

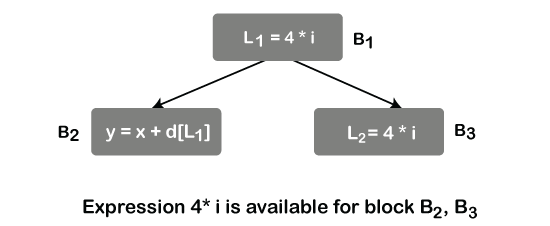
Available Expressions

An expression a + b is said to be available at point p if all the path from entry node p evaluates a + b. There should not be any other assignment to a or b.

We can say that block kills expression a + b if it assigns a or b and does not computes a + b.  

The main use of the available expression is to detect global common sub-expression.