Equivalence of Regular Grammar and Finite Automata

Equivalence of Regular Grammar and Finite Automata

Regular Grammar / type -3 grammar

A regular grammar or type-3 defines the language called regular language that is accepted by finite Automata.A Regular Grammar G consists of 4 tuples (V, T, P, S).

Linear Grammar: Agrammar is called linear in which at most one non-terminal can occur on the right side of any production rule. Following are the types of Linear Grammar:

• Right Linear Grammar
• Left Linear Grammar

Right Linear Grammar: A right linear grammar is a grammar G = (V, T, P, S) such that all the production rules P are one of the following forms:

A -> a

A -> aB

In this, A and B are variables in V i.e. A and B belongs to variable V and a is a terminal. The left-hand side of production rule in right linear grammar consists of only one symbol from set of variables, and right hand side contains either strings of terminals or only one variable present at rightmost position.

Left Linear Grammar: A left linear grammar is a grammar G = (V, T, P, S) such that all the production rules P are one of the following forms:

A -> a

A -> Ba

In this A and B are variables in V i.e. A and B belongs to variables and a is a terminal.

Finite Automata

Finite Automata are the simplest model accepted the language called regular language. The term finite in finite automata is that it has a limited number of states and the limited number of alphabets in the strings. Finite Automata consists of 5 tuples (Q, ?, q₀, F, ?).

The relationship of regular grammar and finite automata is shown below:

Theorem:

If G is a regular grammar then L (G) is a regular language.

Proof:

The regular languages are recognized by finite automata. So, first of all we will construct a NFA equivalent to given right linear grammar which accepts the language defined by the given regular grammar G.

Let G = (V, T, P, S) be a right linear grammar. Let V = {A0A1…..An}, where A0 is the start symbol S. We define an NFA N = ({q0q1….qnqf}, ?, ?, q0, qf}) where ? is defined as:

• For each production Ai -> bAj. In this N has transition from q_i to q_j with label b.
• For each production Ak -> b. In this N has transition from q_k to q_f with label b.

From the construction, it is clear that A0 => b1A1 => b1b2A2 => b1b2b3A3 => …..=>b1bn-1 => b1….bn, if and only if there is a path in N starting from initial state q0 and ends on final state qf with path value b1b2….bn.

Therefore L (G) = T (N).

Example:

Let G = (V, T, P, S) be a regular grammar, where

V = {A0, A1, A2}

T = {0, 1}

S is the start symbol of the grammar.

P is the set of production rules defined as:

A₀ -> 0A₁

A₀ -> 1A₂

A₁ -> 0A₂

A₂ -> 0

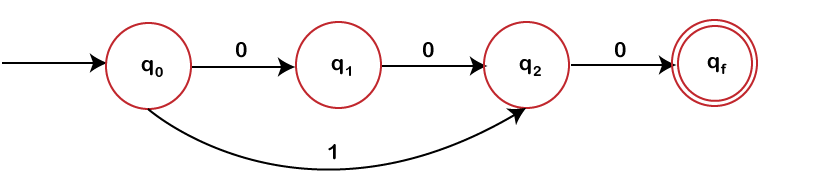
Construct a finite-automata that accepts the language generated by a given grammar G.

Solution:

Let M = (Q, ?, q₀, F, ?) be a finite-automata that accepts L (G), where

Q = {q0, q1, q2, qf}

? = {0, 1}

q0 is the initial state

F = {qf}

The states q0, q1, q2 corresponds to A_0, A_1, A_2, and qf is the new final state of M.

Initially we have 4 states of finite automata M.

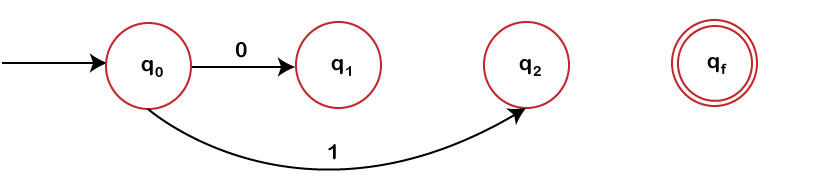
The production rule A₀ -> 0A₁ includes a transition from q0 to q1 with label 0. After this production rule, we have following partial diagram of finite automata.

The production rule A₀ -> 1A₂ includes a transition from q0 to q2 with label 1. After this production rule we have following partial diagram of finite automata.

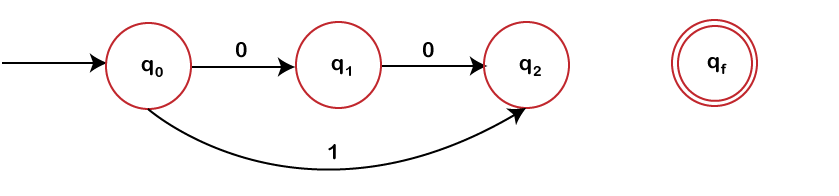
The production rule A₁ -> 0A₂ includes a transition from q1 to q2 with label 0. After this production rule we have following partial diagram of finite automata.

Similarly, for the production rule A₂ -> 0includes a transition from q2 to qf with label 0. After this production rule we have following final diagram of finite automata accepting L (G).