Finite Automata
Finite Automata
Finite state Automata or Finite State Machine is the simplest model used in Automata. Finite state automata accepts regular language. In this, the term finite means it has a limited number of possible states, and number of alphabets in the strings are finite. Finite state Automata is represented by 5 tuples or elements (Q, ?, q 0 , F, ?):
Formal Notation used in the representation of Finite Automata
We can represent Finite automata in two ways, which are given below:
- Transition diagram
The transition diagram is also called a transition graph; it is represented by a diagraph. A transition graph consists of three things:
- Arrow (->): The initial state in the transition diagram is marked with an arrow.
Circle : Each circle represents the state.
Double circle : Double circle indicates the final state or accepting state.
- Transition Table
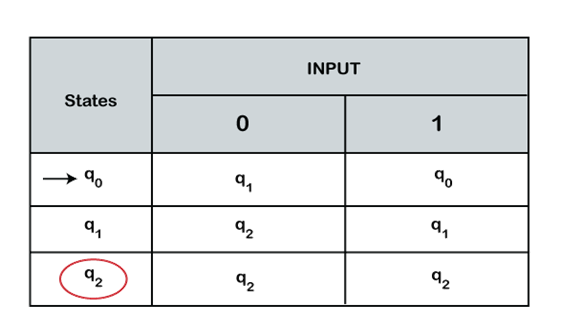
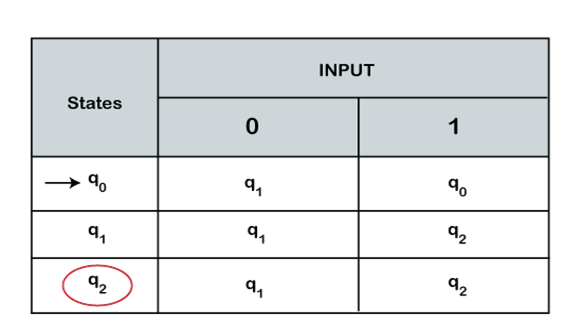
It is the tabular representation of the behavior of the transition function that takes two arguments, the first is a state, and the other is input, and it returns a value, which is the new state of the automata. It represents all the moves of finite-state function based on the current state and input. In the transition table, the initial state is represented with an arrow, and the final state is represented by a single circle. Formally a transition table is a 2-dimensional array, which consists of rows and columns where:
- The rows in the transition table represent the states.
- The columns contain the state in which the machine will move on the input alphabet.
Types of Finite Automata
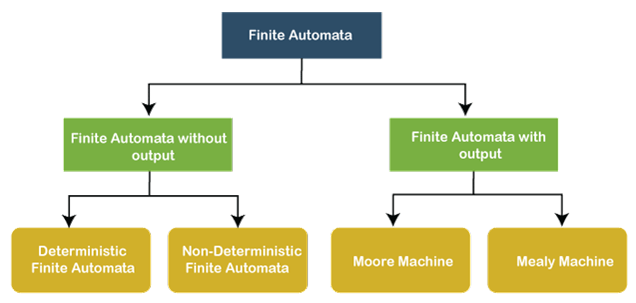
Deterministic Finite Automata
DFA is a short form of Deterministic Finite Automata. In DFA, there is one and only one move from a given state to the next state of any input symbol. In DFA, there is a finite set of states, a finite set of input symbols, and a finite set of transitions from one state to another state that occur on input symbol chosen to form an alphabet; there is exactly one transition out of each state.
Formal Notation of Deterministic Finite Automata (DFA):
A DFA contains 5 tuples or elements (Q, ?, ?, q0, F):
Q: It is a collection of a finite set of states.
?: It is a finite set of input symbols called as the alphabet of the automata.
?: It is used for representing the Transition Function. The states of DFA move from one state to another state in response to some inputs by using the transition function. The transition function given by DFA is given below:
Q x ? -> Q
q0: It is used for representing the initial state of the DFA form where any input is processed.
F: It is a collection of a finite set of final states.
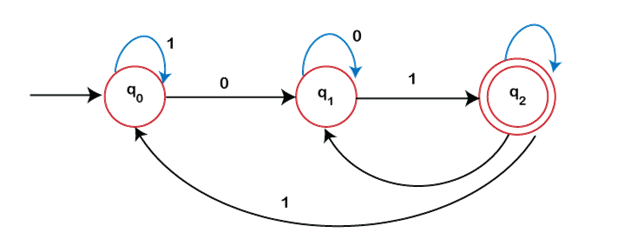
Example of DFA
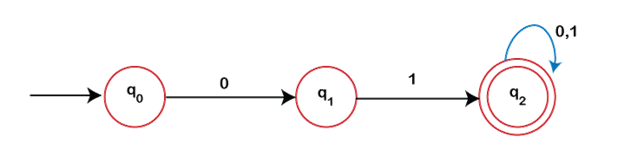
Design a DFA with ? = {0, 1} that accepts those string ending with '01'.
Solution:
L = {01, 010, 110 ……………..} is the language generated.
Q: {q0, q1, q2}, It represents the total number of states
? = {0, 1}
q0 is the initial state
q2 is the final state
Transition diagram
Transition table
Non-Deterministic Finite Automata
NDFA is a short form of Non-Deterministic Finite Automata. In NDFA, there may be more than one move or no move from a given state to the next state of any input symbol. NDFA is a simple machine that is used to recognize the pattern by consuming the string of symbols and alphabets for each input symbol. NDFA differs from DFA in the sense that NDFA can have any number of transitions to the next state from a given state on a given input symbol.
Formal Notation of Non-Deterministic Finite Automata (NDFA):
A NDFA contains 5 tuples or elements (Q, ?, ?, q0, F):
Q: It is a collection of a finite set of states.
?: It is a finite set of input Symbols called the alphabet of the automata.
?: It is used for representing the Transition Function. The states of NDFA move from one state to another state in response to some inputs by using the transition function. The transition function used in NDFA is given below:
?: Q x ? ?2Q
Where 2Q is a power set of Q. In this graph representation of the automata, transition function is represented by arcs between states and the labels on the arcs.
q0: It is used for representing the initial state of the NDFA form where any input is processed.
F: It is a collection of a finite set of final states.
Example of NDFA
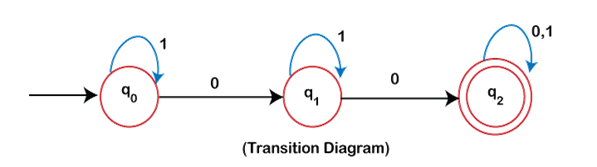
Design a NDFA with ? = {0, 1} that accepts those strings starting with '01'.
Solution:
L = {01, 010, 011 ……………..} is the language generated using this language
Q: {q0, q1, q2}
It represents the total number of states
? = {0, 1}
q0 is the initial state
q2 is the final state
Transition diagram
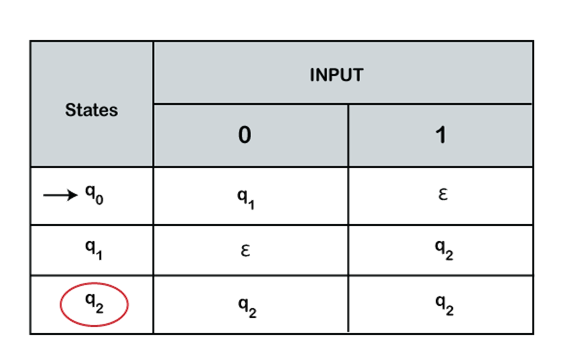
Transition table