Mid-Point Line Drawing Algorithm in Computer Graphics
The Mid-point Subdivision algorithm is the extension of the Cyrus-Beck algorithm. The Mid-Point line plotting algorithm was introduced by “Pitway and Van Aken.” It is an incremental line drawing algorithm. In this algorithm, we perform incremental calculations. The calculations are based on the previous step to find the value of the next point. We perform the same process for each step. By using the mid-point subdivision algorithm, we can draw a line with close approximation between two points. The mid-point subdivision line drawing algorithm subdivides the line at its midpoints continuously.
The Mid-point Subdivision algorithm helps to compute or calculate the visible areas of lines that appear in the window. This line plotting algorithm follows the bisection method to divide the line into equal partitions.
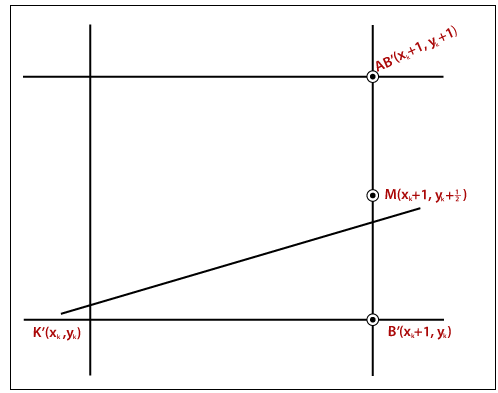
Figure:1
In figure 1, we have a previous point K (xk,yk), and there are two next points; the lower point B (xk + 1,yk) and the above point AB (xk + 1,yk + 1). If the midpoint m is below the line, then we select point AB.
Let us assume, we have two points of the line = (x1, x2) and (y1, y2).
Here, it is (x1< x2)
The Linear equation of a line is:
(x, y) = ax + by +c = 0 …………… (1)
dx =x2 - x1
dy =y2 - y1
As we know, the equation of simple line is:
y = mx +B
Here, m = dy/dx, we can write it as y = (dy/dx) x +B
Put the value of y in above equation, we get
(x, y) = dy (x) - (dx) y +B. dx = 0…………… (2)
By comparing equation (1) and (2)
a = dy
b = -dx
c = B. dx
There are some conditions given-
Condition 1: If all the points are on the line, then (x, y) = 0
Condition 2: If all the points are on the line, then (x, y) = Negative Number
Condition 3: If all the points are on the line, then (x, y) = positive Number
Now, m = (xk +1, yk + 1/2)
d = m = (xk +1, yk + 1/2)
Now, we calculate the distance value (d). Here, we discuss two cases:
Case 1: If
We select the lower point B
Then
The value of d is negative (d < 0)
We calculate the new and old value of d-
dn = (xk +2, yk + 1/2) {The value of x coordinate is incremented by 1}
Place the value of (x, y) in equation (1) andwe got the value of do
dn = a (xk +2) + b (yk + 1/2) + c {New Value of d}
do = a (xk +1) + b (yk + 1/2) + c {Old Value of d}
Thus,
?d = dn – do
= a (xk+2) + b (yk +1/2) + c – a (xk+1) – b (yk +1/2) - c
= a
?d = dn – do
?d = do + a
?d = do +dy {a = dy}
Case 2: If
We select the upper point AB
Then
The value of d is positive (d > 0)
We calculate the new and old value of d-
dn = (xk +2, yk + 3/2) {The value of x and y coordinate is incremented by 1}
We put the value of (x, y) in equation (1) andwe got the value of do
dn = a (xk +2) + b (yk + 3/2) + c {New Value of d}
do = a (xk +1) + b (yk + 1/2) + c {Old Value of d}
Thus,
?d = dn – do
= a (xk+2) + b (yk +3/2) + c – a (xk+1) – b (yk +1/2) - c
= a + b
?d = dn – do
?d = do + a +b
?d = do +dy – dx {a + (-b) = dy- dx}
Now, we calculate the initial decision parameter (di)
di =(x1 +1, y1+ 1/2)
Put the value of di in equation (1)
di = a (x1 +1) + b (y1 + 1/2) + c
= ax1 +a + by1 + b/2 + c
= (x1, y2) + a + b/2
= 0 + a + b/2
di = dy – dx/2
Algorithm of Mid-Point Subdivision Line Drawing
Step 1: Start.
Step 2: Consider the starting point as (x1, y1) and endingpointas (x2, y2).
Step 3: Now, we will calculate ?d.
?d = 2 (?y -?x)
Step 4: Now, we will calculate the decision parameter di with the following formula.
di = 2?y - ?x
Step 5: The increment of x or y coordinate depends on the following two cases-
Case 1: If
di < 0
Then
xk+1 =xk +1
yk+1 = yk
dn = di + 2?y
Case 2: If
di >= 0
Then
xk+1 =xk +1
yk+1 =yk +1
dn = di +?d
Step 6: We will repeat step 5 until we found the ending point of the line.
Step 7: Stop.
Example: A line has a starting point (6,10) and ending point (13,17). Apply the Mid-point Line Drawing algorithm to draw a line.
Solution: We have two coordinates,
Starting Point = (x1, y1) = (6,10)
Ending Point = (x2, y2) = (13,17)
Step 1: First, we calculate ?x, ?y.
?x = x2 – x1 = 13-6 = 7
?y = y2 – y1 = 17-10 = 7
Step 2: Now, we are going to calculate the ?d.
?d= 2(?y-?x)
= 2 (7 – 7) = 0
The value of ?d= 0
Step 3: Now, we will calculate the decision parameter di with following formula.
di = 2?y - ?x
= 2 x 7 – 7 = 7
Step 4: The value of di >= 0. Case 2 is satisfied. Then
xk+1 =xk +1 = 6 +1 = 7
yk+1 =yk +1 = 10 + 1 = 11
dn = di +?d = 7 + 0 = 7
| di | dn | xk+1 | yk+1 |
| 6 | 10 | ||
| 7 | 7 | 7 | 11 |
| 7 | 7 | 8 | 12 |
| 7 | 7 | 9 | 13 |
| 7 | 7 | 10 | 14 |
| 7 | 7 | 11 | 15 |
| 7 | 7 | 12 | 16 |
| 7 | 7 | 13 | 17 |
Step 5: Stop.
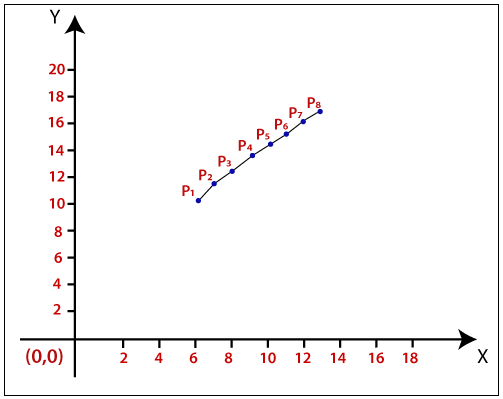
The Coordinates of drawn lines are-
P1 = (6, 10)
P2 = (7, 11)
P3 = (8, 12)
P4 = (9, 13)
P5 = (10, 14)
P6 = (11, 15)
P7 = (12, 16)
P8 = (13, 17)
Advantages of Mid-point Subdivision Line Drawing Algorithm
- It is very easy to implement.
- It is a less time-consuming algorithm.
- This algorithm uses basic arithmetic operations.
- It only requires integer data.
- The drawn line is smooth than other line drawing algorithms.
Disadvantages of Mid-point Subdivision Algorithm
- Sometimes this algorithm is not suitable due to critical images and graphics.
- The points have less accuracy. There are improvements needed.
Related Posts:
- Line Drawing Algorithm in Computer Graphics
- Line Clipping in Computer Graphics
- Filled Area Primitives Computer Graphics
- Midpoint Circle Drawing Algorithm in Computer Graphics
- Bresenham’s Line Drawing Algorithm in Computer Graphics
- Bresenham’s Circle Drawing Algorithm in Computer Graphics
- DDA line Drawing Algorithm in Computer Graphics
- Polygon Clipping in Computer Graphics
- Display Devices in Computer Graphics
- Applications of Computer Graphics