Minimax Strategy
In artificial intelligence, minimax is a decision-making strategy under game theory, which is used to minimize the losing chances in a game and to maximize the winning chances. This strategy is also known as ‘Minmax,’ ’MM,’ or ‘Saddle point.’ Basically, it is a two-player game strategy where if one wins, the other loose the game. This strategy simulates those games that we play in our day-to-day life. Like, if two persons are playing chess, the result will be in favor of one player and will unfavor the other one. The person who will make his best try,efforts as well as cleverness, will surely win.
We can easily understand this strategy via game tree- where the nodes represent the states of the game and edges represent the moves made by the players in the game. Players will be two namely:
- MIN: Decrease the chances of MAX to win the game.
- MAX: Increases his chances of winning the game.
They both play the game alternatively, i.e., turn by turn and following the above strategy, i.e., if one wins, the other will definitely lose it. Both players look at one another as competitors and will try to defeat one-another, giving their best.
In minimax strategy, the result of the game or the utility value is generated by a heuristic function by propagating from the initial node to the root node. It follows the backtracking technique and backtracks to find the best choice. MAX will choose that path which will increase its utility value and MIN will choose the opposite path which could help it to minimize MAX’s utility value.
MINIMAX Algorithm
MINIMAX algorithm is a backtracking algorithm where it backtracks to pick the best move out of several choices. MINIMAX strategy follows the DFS (Depth-first search) concept. Here, we have two players MIN and MAX, and the game is played alternatively between them, i.e., when MAX made a move, then the next turn is of MIN. It means the move made by MAX is fixed and, he cannot change it. The same concept is followed in DFS strategy, i.e., we follow the same path and cannot change in the middle. That’s why in MINIMAX algorithm, instead of BFS, we follow DFS.
- Keep on generating the game tree/ search tree till a limit d.
- Compute the move using a heuristic function.
- Propagate the values from the leaf node till the current position following the minimax strategy.
- Make the best move from the choices.
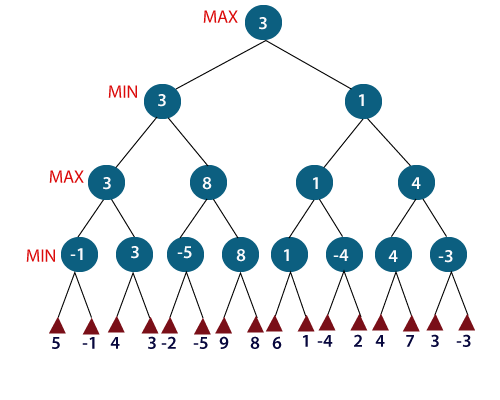
For example, in the above figure, the two players MAX and MIN are there. MAX starts the game by choosing one path and propagating all the nodes of that path. Now, MAX will backtrack to the initial node and choose the best path where his utility value will be the maximum. After this, its MIN chance. MIN will also propagate through a path and again will backtrack, but MIN will choose the path which could minimize MAX winning chances or the utility value.
So, if the level is minimizing, the node will accept the minimum value from the successor nodes. If the level is maximizing, the node will accept the maximum value from the successor.
Note: The time complexity of MINIMAX algorithm is O(bd) where b is the branching factor and d is the depth of the search tree.