Minimization of Finite Automata with Output
Minimization of Finite Automata with Output
The method to minimize the Moore and Mealy machine is very much similar to the method that we have used to minimize the DFA.
Methods to Minimize the Finite Automata with Output
Step1: Detect the unreachable states.
Step2: Eliminate the unreachable states (if find).
Step3: Identify equivalent states and merge them.
Equivalent states can also be found the same way as in the case of minimizing the DFA. But there is only one difference. Initially, we have group A and group B contains the following:
- Group A: All states with a similar type of outputs for all possible inputs.
- Group B: All states with other similar types of outputs for all possible inputs.
Example
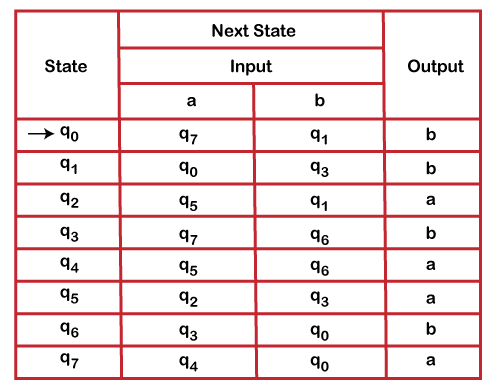
Minimize the following Moore machine.
Solution
Step1: Detect the unreachable states
Start form initial state. Add q0 to temporary state (T)
Initially T = {q0}
?(q0, a) = q7
?(q0, b) = q1
Now, T = {q0, q1, q7}
Again we check all possible states with input a and b.
? (q1, a) = q0
? (q1, b) = q3
? (q3, a) = q7
? (q3, b) = q6
? (q7, a) = q4
? (q7, b) = q0
T = {q0, q1, q3, q4, q6, q7}
Again we check all possible states for input a and b.
? (q4, a) = q5
? (q4, b) = q6
? (q6, a) = q3
? (q6, b) = q0
T = {q0, q1, q3, q4, q5, q6, q7}
Now, again we check all possible states for input a and b.
? (q5, a) = q2
? (q5, b) = q3
? (q2, a) = q5
? (q2, b) = q1
Finally, T = {q0, q2, q1, q3, q4, q5, q6, q7}
U= Q – T
= ? (There is no unreachable state)
Step2: There is no unreachable states to remove.
Step3: Identify equivalent states and merge them.
Initially, we have,
Group A: qo, q1, q3, q6 (contains all states with output b)
Group B: q2, q4, q5, q7 (contains all states with output a)
Now, we check both the groups for both the input symbols. For input symbol a, we have
? (q0, a) = q7
? (q1, b) = q0
? (q3, a) = q7
? (q6, b) = q3
q7 belongs too group B and q0, q3 belongs to group A for input a. since q7 belongs to group B so we partition group A as:
Group A: qo, q3
Group A2: q1, q6
Group B: q2, q4, q5, q7
Now, we check Group B for input a
? (q2, a) = q5
? (q4, a) = q5
? (q5, a) = q2
? (q7, b) = q4
Since q2, q4 and q5 belong to the same Group B. Now for input b, we have
? (q2, b) = q1
? (q4, b) = q6
? (q5, b) = q3
? (q7, b) = q0
q1, q6 belongs to Group A2
q3, q0 belongs to Group A1
After portioning group B, we have
Group A1: qo, q3
Group A2: q1, q6
Group B1: q2, q4
Group B2: q5, q7
Now let us check Group A1 for input a
? (q0, a) = q7
? (q3, a) = q7
q7 belongs to Group B2; for input b, we have
? (q0, b) = q1
? (q3, b) = q6
q1 and q6 belong to Group A2; thus, the further partition of Group A1 is not possible.
Similarly for Group A2
? (q1, b) = q0
? (q6, b) = q3
q0, q3 belongs to Group A1
? (q1, b) = q3
? (q6, b) = q0
q0, q3 belongs to Group A1; thus, the further partition of Group A2 is not possible
Similarly for Group B1
? (q2, a) = q5
? (q4, a) = q5
? (q2, b) = q1
? (q4, b) = q6
q5 belongs to Group B2, and q1 and q6 belongs to Group A2; further partition of Group B1 is not possible
Similarly for Group B2
? (q5, a) = q2
? (q7, a) = q4
? (q5, b) = q3
? (q7, b) = q0
q2, q4 belongs to Group B1 and q0, q3 belongs to Group A1. Thus further portioning of Group B2 is not possible.
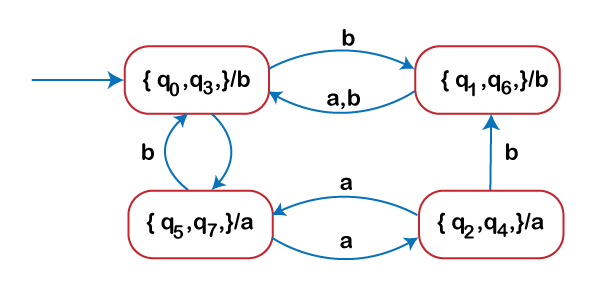
Finally, we have the following partitions:
Group A1: qo, q3
Group A2: q1, q6
Group B1: q2, q4
Group B2: q5, q7
After merging these states, the minimized Moore machine is shown in the following figure: