Polygon Clipping in Computer Graphics
“A Polygon can be described as the enclosed collection or group of the lines.”
In a polygon, all lines are connected. Lines can be a combination of edges and vertices, which together form a polygon. A polygon refers to a two-dimensional architecture made up of a number of straight lines.
Some Examples of the polygon:
- Triangles
- Pentagons
- Hexagons
- Quadrilaterals
The polygon’s name defines how many sides the architecture contains.
Triangle: It has three sides.
Pentagon: A pentagon has five sides.
Hexagon: It contains six sides.
Quadrilaterals: It contains four sides.
Types of Polygon
There are two basic types of polygon-
- Concave Polygon
- Convex Polygon
Concave Polygon: The concave polygon does not have any part of its diagonals in its exterior. In a concave polygon, at least one angle should be greater than 180° (angle >180°).
Convex Polygon: The convex polygon has at least one part of diagonal in its exterior. In a convex polygon, all the angles should be less than 180° (angle<180°).
Polygon Clipping
Polygon clipping is a process in which we only consider the part which is inside the view pane or window. We will remove or clip the part that is outside the window. We will use the following algorithms for polygon clipping-
- Sutherland-Hodgeman polygon clipping algorithm
- Weiler-Atherton polygon clipping algorithm
Sutherland-Hodgeman polygon clipping algorithm
The polygon clipping algorithm deals with four different clipping cases. The output of each case is input for the next case.
Case1) Left clip: In the left side polygon clipping, we only remove the left part of the polygon, which is outside the window. We only save the portion which is inside the window.
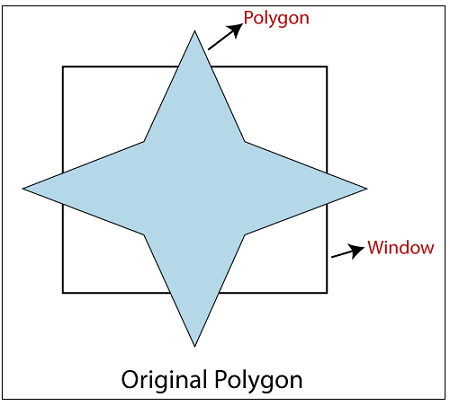
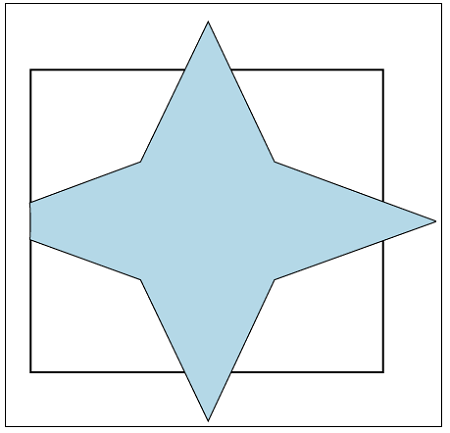
Case2) Right clip: In the right-side polygon clipping, we only remove the right part of the polygon, which is outside the window. We only save the portion which is inside the window.
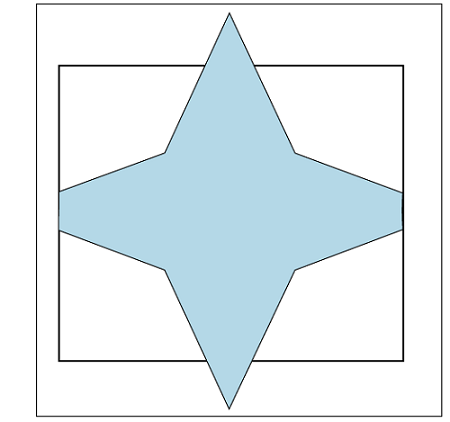
Case3) Top clip: On the top side polygon clipping, we only remove the top part of the polygon, which is outside the window. We only save the portion which is inside the window.
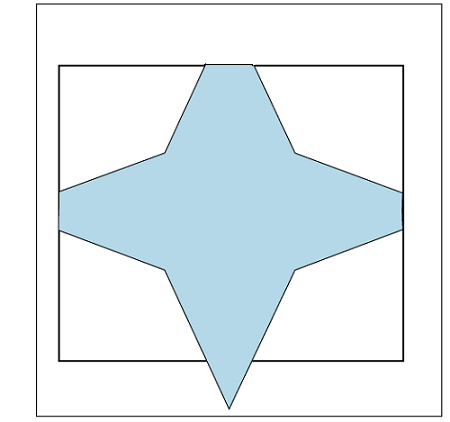
Case4) Bottom clip: In the bottom side polygon clipping, we only remove the bottom part of the polygon, which is outside the window. We only save the portion which is inside the window.
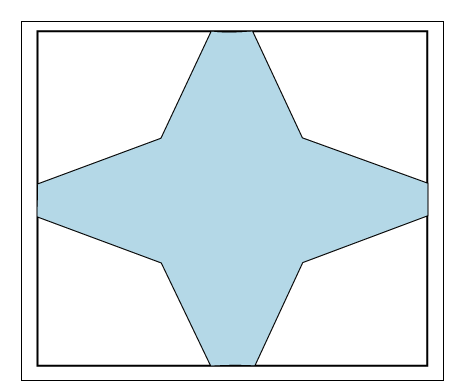
There should be the following conditions while we clip a polygon.
Condition 1(Out-In): If the first vertex of the polygon is outside and the second vertex is inside the window, then the output will be the intersection point and second vertex.
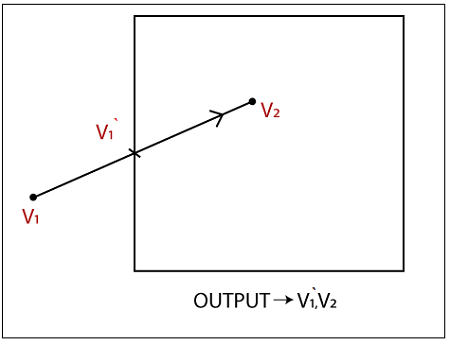
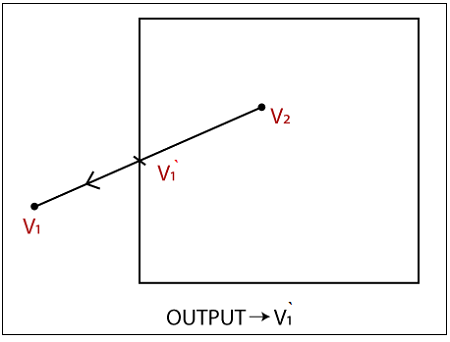
Condition 2(In-Out): If the first vertex of the polygon is inside and the second vertex is outside the window, then the output will be the intersection point.
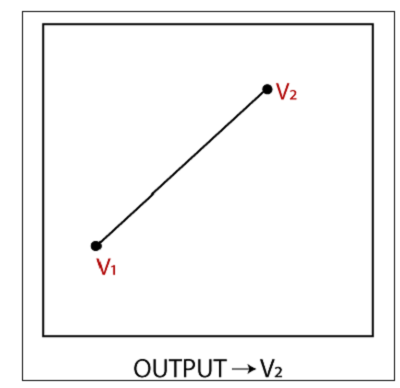
Condition 3(In-In): If both vertices of the polygon are inside the window, then the output will be the second vertex.
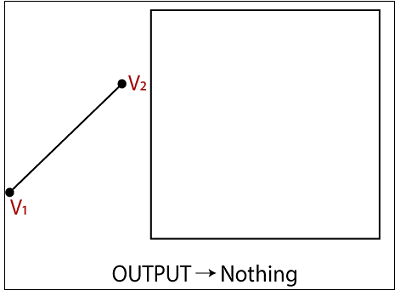
Condition 4(Out-Out): If both vertices of the polygon are outside the window, then the output will be nothing. It means we found a clipped polygon.
Weiler-Atherton polygon clipping algorithm
This algorithm helps us to clip a filled area. The filled area may be a convex polygon or concave polygon. This algorithm was introduced to identify the visible surfaces. This algorithm helps to create individual polygons in some cases. In the Weiler-Atherton algorithm, we consider the view pane boundaries instead of edges and vertices of the polygon.
Algorithm of Weiler-Atherton Polygon Clipping
Step 1: First,create a list of intersection points that are in the starting or ending state. (I1, I2……. In).
Step 2: Now, create twomore lists; one for subject polygon and other for clip polygon.Fill both lists with intersection points and vertices of the polygon.
Order of Subject Polygon list- Write down all the vertices of the polygon in the subject polygon column.
Order of Clip Polygon list – Write down the points of the clipping window.
Step 3: Insert the vertices in both lists in such a way that the intersection point exists between the correct vertices.
Step 4: Now, start from the first vertex of the polygon. Select the first intersection point as an entering point and follow the same process until we reach the exiting point.
Step 5: We can move from clip polygon list to subject polygon list and search for the finishing intersection point. Repeat the process until we find the entering point.
Step 6: Now, the polygon is being clipped. Repeat the same process until each point has been visited once.
Step 7: Stop.
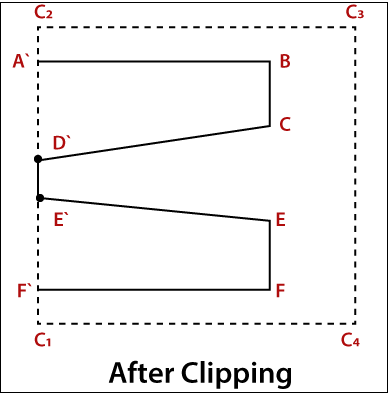
Example: Consider a polygon with vertices ABCDEFG. Apply Weiler- Atherton algorithm to find the clipped polygon?
Solution: Let us assume that the vertices of window = C1, C2, C3, C4
The vertices of polygon = ABCDEFG
First, create two lists, one for subject polygon and second for clip polygon.
Iteration 1-
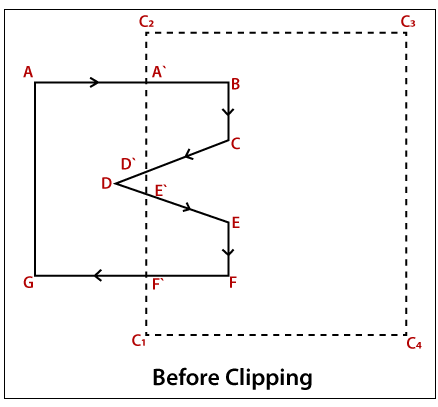
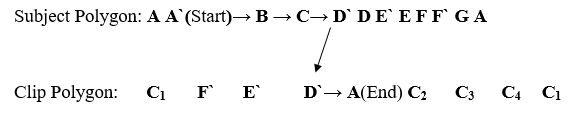
The First new list is- A`, B, C, D`, A`.
Iteration 2-
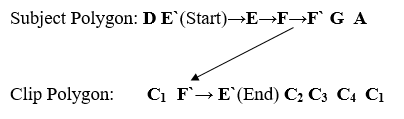
The Second new list is- E`, E, F, F`, F`.
Explanation:
- Check A if it is an intersection point then, start from A otherwise, move to next.
- A` is an intersection point (A` will be saved in the new list) then check the next vertex.
- B is not an intersection point save that in the new list. Then move to next.
- C is also not an intersection point; save it in the new list and move to the next point.
- Now, move to D` (D` is an intersection point). We jump to clip polygon list to find D`.
- We will follow the same procedure for the next iteration.
- This process is repeated until we found the ending point.