Traversal of binary tree
Traversal of binary tree: A node is visited only once in the traversal of the binary tree. There are three main types of traversal methods in the binary tree.
- In-order traversal
- Pre-order traversal
- Post-order traversal
In-order traversal:
In the in-order traversal method, the left child and left subtree are traversed first, afterward the root tree and then the right children or the right subtree are traversed.
Algorithm of In-order traversal
In-order-traversal (tree) Step 1: Start with left sub-tree // call In-order (left subtree) Step 2: Then, root tree Step 3: And then, right sub-tree // call In-order (right subtree)
Example: Find the in-order traversal for this tree.
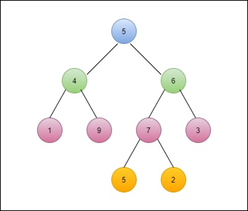
Solution.
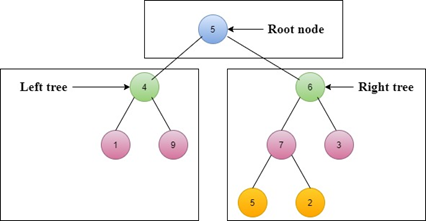
Step 1: Left sub-tree is 1 ? 4 ? 9
Step 2: Root node is 5
Step 3: Right sub-tree is 5 ? 7 ? 2 ? 6 ? 3
In-order Traversal = 1 ? 4 ? 9 ? 5 ? 5 ? 7 ? 2 ? 6 ? 3
Pre-order Traversal:
In the pre-order traversal method, the root node is traversed first, then the left subtree, and then the right subtree is traversed.
Algorithm of pre-order traversal
Pre-order-traversal (tree) Step 1: Start with the root node Step 2: Then, the left sub-tree // call Pre-order (left subtree) Step 3: And then, right sub-tree // call Pre-order (right subtree)
Example: Find the pre-order traversal for this tree.
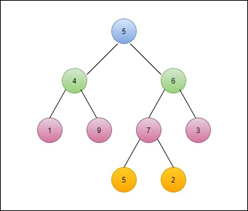
Solution.
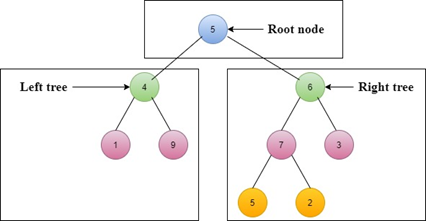
Step 1: Root node is 5
Step 2: Left sub-tree is 4 ? 1 ? 9
Step 3: Right sub-tree is 6 ? 7 ? 5 ? 2 ? 3
Pre-order Traversal = 5 ? 4 ? 1 ? 9 ? 6 ? 7 ? 5 ? 2 ? 3
Post-order traversal:
In the post-order traversal method, the left child and left subtree are traversed first, then the right subtree is traversed, and then the root node.
Algorithm of Post-order traversal
Post-order-traversal (tree) Step 1: Start with left sub-tree // call Post-order (left subtree) Step 2: Then, right sub-tree // call Post-order (right subtree) Step 3: And then, root tree
Example: Find the Post-order traversal for this tree.
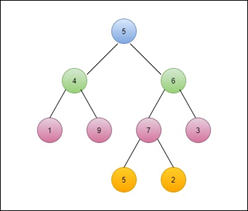
Solution.
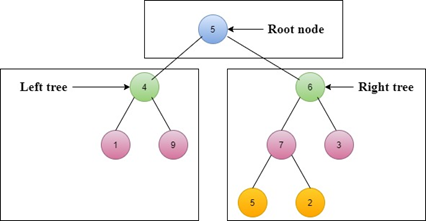
Step 1: Left sub-tree is 1 ? 9 ? 4 Step 2: Right sub-tree is 5 ? 2 ? 7 ? 3 ? 6 Step 3: Root node is 5 Post-order Traversal = 1 ? 9 ? 4 ? 5 ? 2 ? 7 ? 3 ? 6 ? 5
Applications of binary tree
- The binary search tree is used in many search applications.
- Nowadays, a binary Space Partition is used for every 3D game.3.
- The binary tree is used in every high bandwidth router that stores the router table.
Binary tree program in C language
// Binary Tree in C
#include <stdio.h>
#include <stdlib.h>
struct node
{
int data;
struct node *left;
struct node *right;
};
struct node *newNode(int data)
{
struct node *node = (struct node *)malloc(sizeof(struct node));
node->data = data; node->left = NULL;
node->right = NULL; return (node); }
void traversePreOrder(struct node *t)
{
if (t != NULL)
{
printf(" %d", t->data);
traversePreOrder(t->left);
traversePreOrder(t->right);
}
}
void traverseInOrder(struct node *t)
{
if (t != NULL)
{
traverseInOrder(t->left);
printf(" %d", t->data);
traverseInOrder(t->right);
}
}
void traversePostOrder(struct node *t)
{
if (t != NULL)
{
traversePostOrder(t->left);
traversePostOrder(t->right);
printf(" %d", t->data);
}
}
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
printf("The preorder traversal of the tree is: ");
traversePreOrder(root);
printf("\nThe inorder traversal of the tree is: ");
traverseInOrder(root);
printf("\nThe postorder traversal of the tree is: ");
traversePostOrder(root); }