YACC in Compiler Design
YACC
YACC is known as Yet Another Compiler Compiler. It is used to produce the source code of the syntactic analyzer of the language produced by LALR (1) grammar. The input of YACC is the rule or grammar, and the output is a C program. Stephen C. Johnson creates the first kind of YACC. If we have a file translate.y that consists of YACC specification, then the UNIX system command is:
YACC translate.y
This command converts the file translate.y into a C file y.tab.c. It represents an LALR parser prepared in C with some other user’s prepared C routines. By compiling y.tab.c along with the ly library, we will get the desired object program a.out that performs the operation defined by the original YACC program.
The construction of translation using YACC is illustrated in the figure below:
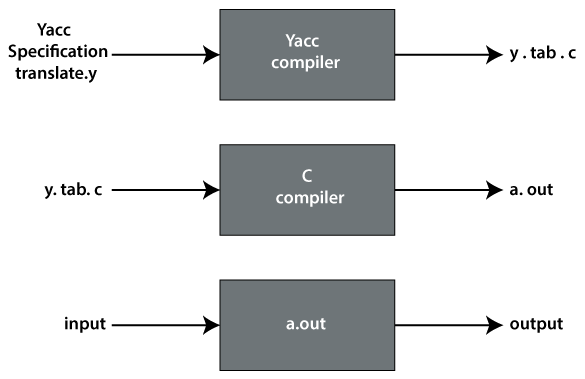
A YACC source program contains three parts:
- Declarations
%%
- Translation rules
%%
- Supporting C rules
Declarations Part
This part of YACC has two sections; both are optional. The first section has ordinary C declarations, which is delimited by %{ and %}. Any temporary variable used by the second and third sections will be kept in this part. See the below code:
%{
#include <ctype.h>
%}
%token DIGIT
%%
line : expr ‘\n’ { printf("%d\n", $1); }
;
expr : expr '+' term { $$ = $1 + $3; }
| term
;
term : term '*' factor { $$ = $1 * $3; }
| factor
;
factor : ‘(‘ expr ’)’ { $$ = $2; }
| DIGIT
;
%%
yylex() {
int c;
c = getchar();
if (isdigit(c)) {
yylval = c-'0';
return DIGIT;
}
return c;
}
In the above code, the declaration part only contains the include statement.
#include <ctype.h>
Declaration of grammar tokens also comes in the declaration part.
%token DIGIT
This part defined the tokens that can be used in the later parts of a YACC specification.
Translation Rule Part
After the first %% pair in the YACC specification part, we place the translation rules. Every rule has a grammar production and the associated semantic action.
A set of productions:
<head> => <body>1 | <body>2 | ..... | <body>n
would be written in YACC as
<head> : <body>1 {<semantic action>1}
| <body>2 {<semantic action>2}
.....
| <body>n {<semantic action>n}
;
In a YACC production, an unquoted string of letters and digits that are not considered tokens is treated as non-terminals.
The semantic action of YACC is a set of C statements. In a semantic action, the symbol $$ considered to be an attribute value associated with the head's non-terminal. While $i considered as the value associated with the ith grammar production of the body.
If we have left only with associated production, the semantic action will be performed. The value of $$ is computed in terms of $i's by semantic action.
Supporting C–Rules
It is the last part of the YACC specification and should provide a lexical analyzer named yylex(). These produced tokens have the token's name and are associated with its attribute value. Whenever any token like DIGIT is returned, the returned token name should have been declared in the first part of the YACC specification.
The attribute value which is associated with a token will communicate to the parser through a variable called yylval. This variable is defined by a YACC.
Whenever YACC reports that there is a conflict in parsing-action, we should have to create and consult the file y.output to see why this conflict in the parsing-action has arisen and to see whether the conflict has been resolved smoothly or not.
Instructed YACC can reduce all parsing action conflict with the help of two rules that are mentioned below:
- A reduce/reduce conflict can be removed by choosing the production which has conflict mentioned earlier in the YACC specification.
- A shift/reduce conflict is reduced in favor of shift. A shift/reduce conflict that arises from the dangling-else ambiguity can be solved correctly using this rule.