In graph theory, a graph is a collection of vertices (also known as nodes) and edges. Edges are the lines that connect the vertices and are used to represent relationships between them.

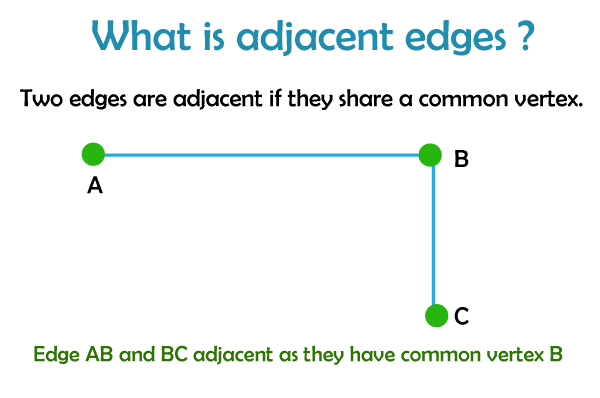
Two edges in a graph are considered to be adjacent if they share a common endpoint or vertex. This means that the two edges are connected to the same vertex. For example, in the following graph, the edges (A, B) and (A, C) are adjacent because they both share the vertex A.

Graph

A -- B
|\ |
| \ |
| |
C -- D

We can also say that two edges are adjacent if they are incident to the same vertex, which means that they share the vertex but not necessarily the direction.

In graph theory, the concept of adjacent edges is used in several ways. For example, adjacent edges can be used to measure the degree of a vertex, which is the number of edges that are incident to that vertex. Adjacent edges can also be used to measure the connectivity of a graph, which is the number of edges that need to be removed to disconnect the graph.

In some graphs, like trees, connected components, the adjacent edges are more related in the sense that they are connected to the same vertex, but they are also connected to other vertex, making a path between two vertexes.

Importance of Adjacent Edges

Adjacent edges are important in planar graphs which are graphs that can be drawn on a flat surface without any of the edges crossing each other. In a planar graph, two edges are considered adjacent if they share an endpoint, but they also cross each other.

Adjacent edges are important in many aspects of graph theory, and understanding them is crucial for studying and analyzing graphs.

Adjacent edges can play a role in graph algorithms. For example, in shortest path algorithms like Dijkstra's algorithm or A*, the adjacent edges of a vertex are used to determine the next step in the path.

Adjacent edges can also be used in topological sorting algorithms, which are used to order the vertices in a directed acyclic graph (DAG) in a way that all the edges point from earlier vertices to later vertices.

Adjacent edges can be useful in clustering algorithms like Spectral Clustering, and in hierarchical clustering, where adjacent edges are used to group similar vertices together.

It's also related with the concept of degree of a vertex which is defined as the number of edges incident to the vertex, this mean that the degree of a vertex is calculated as the number of adjacent edges that the vertex has.

In some cases, adjacent edges can be used to define graph's properties, like

a graph is regular if each vertex of the graph has the same degree and it's sparse if the degree of each vertex is low compared to the number of vertices on the graph.

Note: Adjacent edges are a fundamental concept in graph theory, and understanding how they work and how to use them can help you analyze, understand, and solve problems related to graphs.

Here's an example of a graph that illustrates the concept of adjacent edges:

Graph:

A----B
/ \ |
/ \ |
C-----D |
\ / |
\ / |
E----F

In this graph, there are 6 vertices (A, B, C, D, E, F) and 8 edges. Some examples of adjacent edges in this graph are:

(A, B) and (A, C) are adjacent because they share the vertex A.
(C, E) and (E, F) are adjacent because they share the vertex E.
(B, D) and (C, D) are adjacent because they share the vertex D.

We can also notice that vertex A has degree of 3, which means that it is connected to 3 edges. Similarly, vertex B has degree 2, vertex C has degree 3 and so on. We can see that this graph is not regular because the vertices have different degree.

Also, there are multiple paths that connect vertex A to vertex F for example.

Like: A-B-D-F or A-C-D-F.

Additionally, this graph is sparse because the number of edges is significantly lower than the number of possible edges. In total, there could be 15 edges in a fully connected graph with 6 vertices.

Properties of Adjacent edges in graph theory

In graph theory, two edges in a graph are considered adjacent if they share a common endpoint. Adjacent edges can have several properties that are important in graph analysis and algorithms.

Parity: Adjacent edges can have the same or different parity. A pair of edges is said to have the same parity if they both connect the same pair of vertices, and different parity if they connect different pairs of vertices.
Orientation: Adjacent edges can have the same or different orientations. Two edges are said to have the same orientation if they are both directed or both undirected. If one edge is directed and the other is undirected, they are said to have different orientations.
Length: Adjacent edges can have the same or different lengths. The length of an edge is defined as the distance between the two vertices it connects. Two edges are said to have the same length if they have the same distance between their endpoints and different length if they have different distances.
Weight: Adjacent edges can have the same or different weights. The weight of an edge is a numerical value assigned to it, which can represent the cost of traversing the edge or a measure of its importance. Two edges are said to have the same weight if they have the same numerical value assigned to them, and different weight if they have different numerical values.
Connectivity: Adjacent edges can increase or decrease the connectivity of a graph. An edge that connects two previously disconnected vertices increases the connectivity of the graph, while an edge that disconnects two previously connected vertices decreases the connectivity of the graph.
Multiplicity: Adjacent edges can have the same or different multiplicity. The multiplicity of an edge is the number of times it appears in the graph. Two edges are said to have the same multiplicity if they appear the same number of times in the graph and different multiplicity if they appear different number of times.
Type: Adjacent edges can be of the same or different types. Edges can be classified based on different criteria such as the type of vertex they connect (e.g., regular or special), the relationship between the vertices they connect (e.g., parent-child or friend-friend), or the properties of the vertices they connect (e.g., degree or centrality).

Rules for adjacent edges in graph theory

In graph theory, the rules for adjacent edges include:

Adjacency: Two edges are considered adjacent if they share a common endpoint. This is the most basic rule for determining if edges are adjacent.
Connectivity: Adjacent edges can either increase or decrease the connectivity of a graph. An edge that connects two previously disconnected vertices increases the connectivity of the graph, while an edge that disconnects two previously connected vertices decreases the connectivity of the graph.
Cut edges: An edge is considered a cut edge or bridge if its removal increases the number of connected components in a graph.
Multiplicity: Adjacent edges can have the same or different multiplicity, which is the number of times an edge appears in the graph.
Orientation: Adjacent edges can have the same or different orientations, meaning they can be directed or undirected.
Parity: Adjacent edges can have the same or different parity, which is determined by whether the edges connect the same or different pairs of vertices.
Self-loop: A self-loop is an edge that connects a vertex to itself, and it's not allowed in simple graphs but it is allowed in pseudo graphs.
Parallel edges: In a graph, two edges are considered parallel if they have the same endpoints and the same direction. Parallel edges are not allowed in simple graphs but they are allowed in multigraphs.

These rules provide a framework for understanding and analyzing the relationships between edges in a graph, and are commonly used in graph algorithms and analysis.

Conclusion

In summary, understanding the concept of adjacent edges in graph theory is crucial for analyzing and solving problems related to graphs. Adjacent edges share a common endpoint, and their properties such as parity, orientation, length, weight, connectivity, multiplicity, type, label, and color can have different implications for graph analysis and algorithms. There are also several rules that apply to adjacent edges in a graph, such as the handshaking lemma, cut edges, parallel edges, self-loops, adjacency matrix, incidence matrix and adjacency list, which are used to represent and analyze the graph. The choice of representation depends on the specific problem and the desired trade-offs between space and time complexity. In conclusion, understanding the properties and rules of adjacent edges in graph theory is essential for solving different graph problems and understanding graph-related concepts.

Graph Theory Index