Conversion from NFA to DFA
Conversion from NFA to DFA
A Non-deterministic Finite Automata (NFA) is a finite state machine, in which, the move from one state to another is not fully deterministic, i.e., for a particular symbol, there may be more than one moves leading to different states.
There are two ways of conversion from NFA to DFA, which are given below:
- Conversion from NFA to DFA using Transition Table
- Conversion from NFA to DFA using Transition diagram
Conversion from NFA to DFA using Transition Table
In this method, we convert NFA to DFA by using the transition table of NFA. The entries in the transition table for DFA under the input symbol(s) are in square brackets, e.g. [q0, q1], which specifies a set, i.e., a single state whose elements are the different states of NFA.
While converting NFA to DFA, all DFA states occupy a final state of NFA as a member of its final state and the first state in the state’s column in the transition table of NFA is assigned as the initial state of DFA.
Example
Find the DFA equivalent to the given NFA whose transition table is given below:

Solution
Firstly, we construct the transition table of DFA from the transition table of NFA. The first row of the transition table will be the same as the NFA transition table. The partial transition table of DFA is given below:
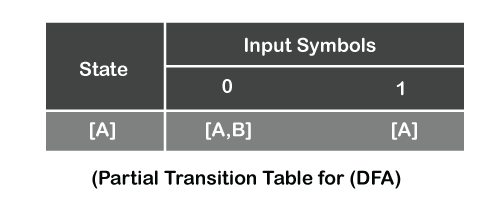
Now, we have two states [A, B] and [A] on the left side of the table in the state column. All the states that appear in the symbol column must appear in state column. So, we write [A, B] in the left column of the next row
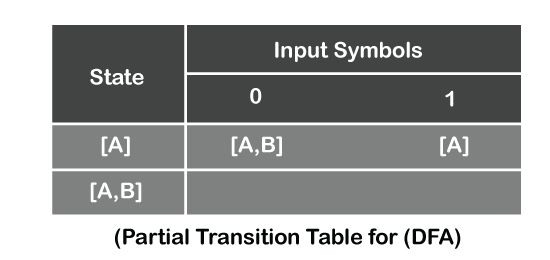
Now we find transitions on the state [A, B] for input symbols 0 and 1. To find these transitions, use the transition table of NFA. On input 0 from state A, we can move to state A, B and on input 0 from state B, we can move to state C. In DFA, on input 0 from state [A, B], we can move to state [A, B, C]. This step follows for all states of DFA.
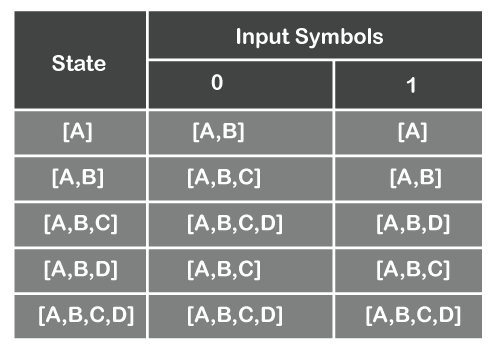
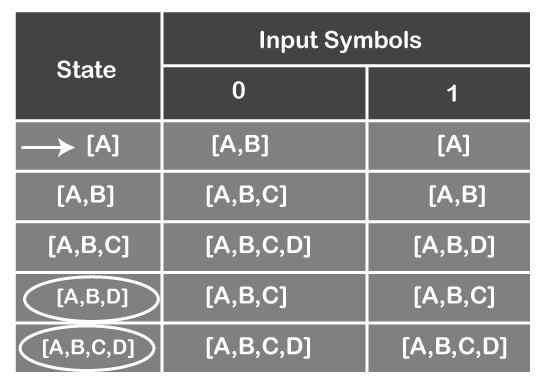
We stop these steps when there are no more states under the input columns. Now we will mark the initial and final states of DFA. In NFA, we have D as the final state. So, in DFA, every state where D appears will be the final state. And the first row [A] of the transition table of DFA will be marked as the initial state.
Following is the transition table of DFA
Conversion from NFA to DFA using Transition diagram
In this, if we are given a transition table of NFA, then first we will draw the transition diagram of NFA from the transition table of NFA. There are various steps for converting NFA to DFA, which are given below:
Step1: Create a transition diagram with the initial state of NFA. For example, suppose {q0} as an initial state. Mark it as the initial state of DFA.
Step2: Repeat the following steps until no more edges are missing.
Take any vertex {qi, qj, …qk} of Transition diagram that has no transitions specified for some input alphabet 0.
- Compute ? (qi, 0) U ? (qj, 0) U ………………… U ? (qk,0)
Let the result of these transitions after union is {ql, qm …qn}
- Create a vertex (new state) labeled {ql, qm …qn}, if it does not already exist in the transition diagram of DFA.
- Add an edge labeled b from state {qi, qj …qk} to state {ql, qm …qn} to Transition diagram
Step3: Every state of the Transition diagram in which the final state of NFA appears, make it the final state.
Example
Convert the following NFA to DFA
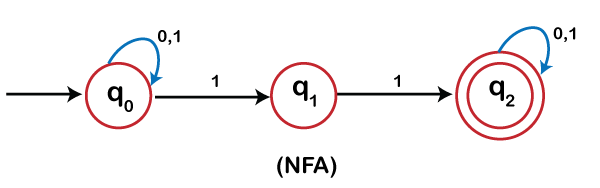
Solution
Step1: We have initial state q0 in NFA. It means in DFA, we have {q0} as start state create a vertex for {q0}.
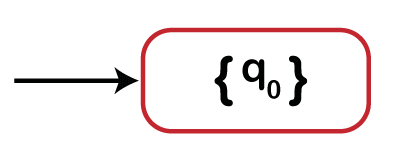
Step2: In the second step, we find transitions on input 0 and 1 from state {q0}.
? ({q0}, 0) = {q0}
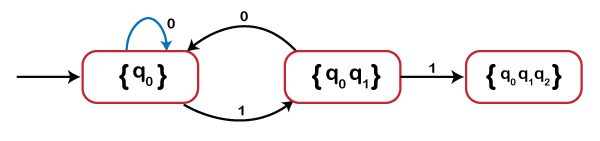
In this step, no need to create a vertex in the diagram because vertex {q0} already exists. So, in this, we simply add a self-loop from state {q0} with label 0.
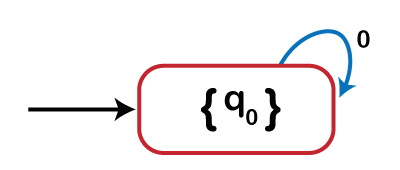
Again we find
? ({q0}, 1) = {q0,q1}
Create a new vertex as shown below
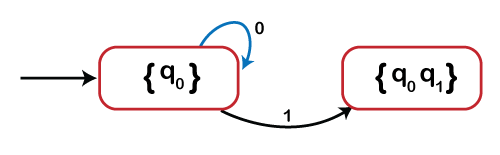
Now, we will find transitions from state {q0, q1}
? ({q0,q1}, 0) = ? (q0,0) U ? (q1,0)
= {q0}
? ({q0,q1}, 1) = ? (q0,1) U ? (q1,1)
= {q0, q1, q2}
Now, create a new vertex as shown below
Now, we will find transitions from state {q0, q1, q2}
? ({q0,q1,q2}, 0) = ? (q0,0) U ? (q1,0) U ? (q2,0)
= {q0, q2}
? ({q0,q1,q2}, 1) = ? (q0,1) U ? (q1,1) U ? (q2,1)
= {q0, q1, q2}
Again create a new vertex

Now, we will find transitions from state {q0, q2}
? ({q0,q2}, 0) = ? (q0,0) U ? (q2,0)
= {q0, q2}
? ({q0,q2}, 1) = ? (q0,1) U ? (q2,1)
= {q0, q1, q2}
The moves are shown below

The vertex {q0, q2} and {q0, q1, q2} contains q2, which is the final state of NFA. So, these are also the final states of DFA.
The final DFA is shown below.
