What is Automata Theory?
What is Automata Theory?
Automata theory is used to study the abstract machine and automata (the self-acting machine). Abstract machine is a theoretical model of a computer used in Automata theory. Automata theory is used to solve the computational problems. Abstract devices are easiest models of real calculations or computations. The basic meaning of “Automata” means "self-making” which is taken from the word “????????”. Automata used in various fields like:
- Theory of computation
- Compiler construction
- Artificial intelligence,
- Parsing
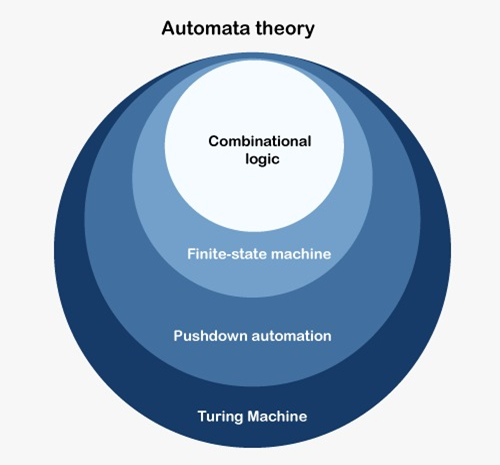
The basic terminologies used in Automata Theory
- Alphabets
- Strings
- Languages
- Grammars
Alphabets:
An alphabets is a finite set of non-empty symbols. The symbol ? (sigma) is used to denote an alphabet.
Examples:
? = {0, 1} is the binary alphabet
? = {a, b, c… z} is the set of lowercase letters
? = {A, B, C… Z} is the set of uppercase letters
?= {(, )}: the set of open and closed brackets
Strings:
A string is a finite sequence of symbols selected from alphabets.
Examples:
abcbz is a string over ? = {a, b, c, d… z}
11001011 is a string over ? = {0, 1}
)) ()(() is a string over ? = {(,)}
Kleene Star (Closure)
The Kleene star ?* includes the all possible strings of lengths over ? including the empty string ? or ?. It is represented by using below notation:
?* = ?0 ? ?1 ? ?2 ?……. ?n
Example:
? = {1, 2}
?* = {?, 1, 2, 11, 22, 12, 21…}
Kleene Star (Plus)
The set ?+ is the infinite set of all possible strings of lengths over ? excluding ? or ?. In simple words it does not include empty string.
It is represented by using below notation:
?+ = ?1 ? ?2 ? ?3 ?…….?n
?+ = ?* ? {?}
Example
? = {1, 2}
?+ = {1, 2, 11, 22, 12, and 21…}
Empty or Null String
The strings having no symbol is called the empty string and null string. Empty string is the string with zero or no occurrence of symbols in the given string. The general notation of representing empty string is ?.
Reverse of String
The reverse of string WR is calculated by writing symbols in reverse order.
Example
“automata” is the string
WR = “atamotua” is the reverse of string
Substring
A string of consecutive characters from W is called as substring of W.
Example
W = bbababa be a string over an alphabet ? = {a, b} then a, bba, aba are substrings of w.
Length of String
The number of symbols in a string defines the length of the string. Length of a string w, denoted by “|w|”, is equal to the number of (non- ?) characters in the string.
Example:
W = 010100
No of string |W| = 6
Concatenation of Strings
The Concatenation of Strings is used to join and concatenate the two or more strings. Suppose ‘a’ and ‘b’ are the strings, then Concatenation of strings will be ‘ab’.
Example:
“Hello” is a string and “World” is another string
The Concatenation of Strings is HelloWorld
Palindrome String
A palindrome is the string which is same as whether it is written forward or backward.
Examples:
Madam is a palindrome string
131 is a palindrome string
Language
A language is a set of strings or symbols from some alphabet. A language is collection of strings. A language can be finite or infinite also.
Examples:
The language L of strings of length 2, defined over ?= {a, b, c}, can be written as
L= {aa, ab, ac, ba, bb, ac, ca, cb, cc}
The complement of language is denoted by L’, it is calculated by using
L' = ?* - L.
Grammar
A grammar defines a set of rules, and with the use of these rules, valid sentences in a language are generated. Similar to English language we have set of rules in automata, which help us in creating sentences. A popular way to derive a grammar recursively is phrase-structure grammar.
Example
A derivation of “The girl sleeps” <Sentence> => <noun-phrase> <predicate> => <noun-phrase> <verb> => <article> <noun> <verb> => The <noun> <verb> => The girl <verb> => The girl sleeps