Backward Chaining in AI: Artificial Intelligence

Backward Chaining is a backward approach which works in the backward direction. It begins its journey from the back of the goal.

Like, forward chaining, we have backward chaining for Propositional logic as well as Predicate logic followed by their respective algorithms.

Let’s discuss both types one by one:

Backward Chaining in Propositional Logic

In propositional logic, backward chaining begins from the goal and using the given propositions, it proves the asked goal. There is a backward chaining algorithm which is used to perform backward chaining for the given axioms. The first algorithm given is known as the Davis-Putnam algorithm. It was proposed by Martin Davis and Hilary Putnam in 1960. In 1962, Davis, Logemann and Loveland presented a new version of the Davis-Putnam algorithm. It was named under the initials of all four authors as DPLL. The versioned algorithm (DPLL) takes an input of a statement as CNF.

The DPLL algorithm is as follows:

function DPLL-SATISFIABLE?(s) returns true or false
inputs: s, a sentence in propositional logic
clauses ? clause set  in CNF representation of s
symbols?list of proposition symbols in s
return DPLL(clauses, symbols,{ })
function DPLL(clauses, symbols,model ) returns true or false
if every clause is true in model then return true
if some clause is false in model then return false
P, value?FIND-PURE-SYMBOL(symbols, clauses,model )
if the value of P is non-null then return DPLL(clauses, symbols – P,model ? {P=value})
P, value?FIND-UNIT-CLAUSE(clauses,model )
if the value ofP is non-null then return DPLL(clauses, symbols – P,model ? {P=value})
P ?FIRST(symbols); rest ?REST(symbols)
return DPLL(clauses, rest ,model ? {P=true}) or
DPLL(clauses, rest ,model ? {P=false}))                                                                                               

Note: The above backward chaining algorithm is used to check satisfiability of a sentence in propositional logic.

Why was DPLL introduced?

There are following improvements required in the Davis-Putnam algorithm, which led to the introduction of the DPLL algorithm:

• Early Termination: The algorithm used to detect if the sentence must be true or false, even if it is a partially completed model.
• Pure symbol heuristic: It is the symbol which always appears with the same sign in each clause.
• Unit clause heuristic: It was defined earlier as a clause with just one literal. In DPLL, it also means clauses in which all literals excluding one is already assigned with a false value in the model.

The above algorithm is limited to small problems.

But for large problems, we have some specific  tricks described below:

• Component analysis: DPLL assigns true values to variables, therefore set of clauses may become disjoint subsets. They are known as components which share no unassigned variables. Provided an efficient method to detect, the solver can solve each component separately.
• Variable and value ordering:  in the above DPLL algorithm, we have used an arbitrary variable and always tried to make the value true first. Degree heuristic helps in doing so.
• Intelligent Backtracking: The problem which cannot be solved in hours can easily be solved in few minutes by applying intelligent backtracking.
• Random restarts: Restarting from the initial state, we can have random decisions regarding the direction to be chosen to reach the goal. Like, in hill-climbing, we can restart from the top to reach the goal  in a more efficient way.
• Clever indexing: The fast indexing methods helps to process the backtracking fastly.

Example of Backward Chaining in Propositional Logic

Let’s consider the previous section  example:

Given that:

1. If D barks and D eats bone, then D is a dog.
2. If V is cold and V is sweet, then V is ice-cream.
3. If D is a dog, then D is black.
4. If V is ice-cream, then it is Vanilla.

Derive backward chaining using the given known facts to prove Tomy is black.

• Tomy barks.
• Tomy eats bone.

Solution:

1. On replacing D with Tomy in (3), it becomes:

If Tomy is a dog, then Tomy is black.

           Thus, the goal is matched with the above axiom.

• Now, we have to prove Tomy is a dog.                                  …(new goal)

     Replace D with Tomy in (1), it will become:

If Tomy barks and Tomy eats bone, then Tomy is a dog.        …(new goal)

Again, the goal is achieved.

• Now, we have to prove that Tomy barks and Tomy eats bone.       …(new goal)

      As we can see, the goal is a combination of two sentences which can be further divided as:

Tomy barks.

Tomy eats bone.

From (1), it is clear that Tomy is a dog.

Hence, Tomy is black.

Note: Statement (2) and (4) are not used in proving the given axiom. So, it is clear that goal never matches the negated versions of the axioms. Always Modus Ponen is used, rather Modus Tollen.

Backward Chaining in FOPL

In FOPL, backward chaining works from the backward direction of the goal, apply the rules on the known facts which could support the proof. Backward Chaining is a type of AND/OR search because we can prove the goal by applying any rule in the knowledge base. A backward chaining algorithm is used to process the backward chaining.

The algorithm is given below:

function FOL_BACKWARD_ASK(KB, query) returns  generator of the substitutions
return FOL_BACKWARD_OR(KB, query,{ })
generator FOL_BACKWARD_OR(KB, goal , ?) yields the substitution
for each (lhs ? rhs) rule in FETCH-RULES-FOR-GOAL(KB, goal ) do
(lhs, rhs)?STANDARDIZE-VARIABLES((lhs, rhs))
for each ? in FOL_BACKWARD_AND(KB, lhs, UNIFY(rhs, goal , ?)) do
yield ?_
generator FOL_BACKWARD_AND(KB, goals, ?) yields a substitution
if ? = failure then return
else if LENGTH(goals) = 0 then yield ?
else do
first,rest ?FIRST(goals), REST(goals)
for each ? in FOL_BACKWARD_OR(KB, SUBST(?, first), ?) do
for each ? in FOL_BACKWARD_AND(KB, rest , ?_) do
yield 

Above illustrated is a simple backward chaining algorithm under FOPL.

Example of Backward Chaining in FOPL

Let’s solve the previous section example of Forward Chaining in FOPL using Backward Chaining.

Consider the below axioms:

1) Gita loves all types of clothes.

2) Suits are clothes.

3) Jackets are clothes.

4)Anything any wear and isn’t bad is clothes.

5) Sita wears skirt and is good.

6) Renu wears anything Sita wears.

Apply backward chaining and prove that Gita loves Kurtis.

Solution: Convert the given axioms into FOPL as:

1. x: clothes(x)?loves(Gita, x).
2. Suits(x)?Clothes(x).
3. Jackets(x)?Clothes(x).
4. wears(x,y)?? ¬bad(y)?Clothes(x)
5. wears(Sita,skirt)? ¬good(Sita)
6. wears(Sita,x)?wears(Renu,x)

To prove: Gita loves Kurtis.

FOPL: loves(Gita, Kurtis).

Apply backward chaining in the below graph: 

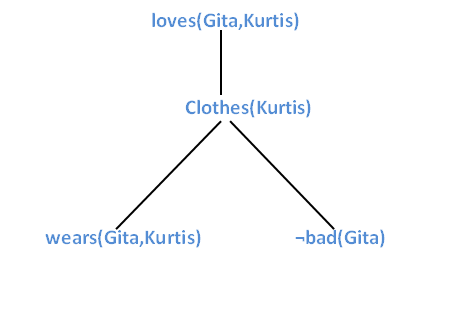
It is clear from the above graph Gita wears Kurtis and does not look bad. Hence, Gita loves Kurtis.

Note: We have seen that the graph of forward and backward chaining is same. It means that forward chaining follows the bottom-up approach and backward chaining follows the top-down approach.