Hidden Markov Models

Hidden Markov Model is a partially observable model, where the agent partially observes the states. This model is based on the statistical Markov model, where a system being modeled follows the Markov process with some hidden states. In simple words, it is a Markov model where the agent has some hidden states. L.E. Baum and coworkers developed the model.

Markov Process

The HMM model follows the Markov Chain process or rule. This process describes a sequence of possible events where probability of every event depends on those states of previous events which had already occurred. Andrey Markov, a Russian mathematician, gave the Markov process. The Markov chain property is:

P(S_ik|S_i1,S_i2,…..,S_ik-1) = P(S_ik|S_ik-1), where S denotes the different states.

Markov Models

Markov model is a stochastic model which is used to model the randomly changing systems. The assumption is that the future states depend only on the current state, and not on those events which had already occurred. Such type of model follows one of the properties of Markov.

The process followed in the Markov model is described by the below steps:

• Carries a set of states: {s₁, s₂,….s_N}
• Sequence of states is generated as {s_i1, s_i2,….,s_ik,….}, when the process moves from one state to the other.
• Follows the Markov Chain property (described above)
• The probabilities which need to be specified to define the Markov model are the transition probabilities and the initial probabilities.

Transition Probability, a_ij = P(s_i | s_j), and

Initial Probability, ?_i = P(s_i)

Example of Markov Models(MM)

Consider the given probabilities for the two given states: Rain and Dry.

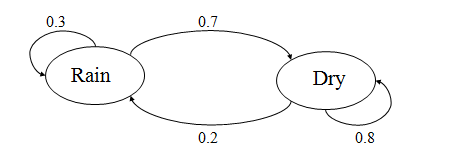
The initial probabilities for Rain state and Dry state be:

P(Rain) = 0.4, P(Dry) = 0.6

The transition probabilities for both the Rain and Dry state can be described as:

P(Rain|Rain) = 0.3, P(Dry|Dry) = 0.8

P(Dry|Rain) = 0.7, P(Rain|Dry) = 0.2 .

Now, if we want to calculate the probability of a sequence of states, i.e., {Dry,Dry,Rain,Rain}.

It will be calculated as:

 P({Dry, Dry, Rain, Rain}) = P(Rain|Rain) . P(Rain|Dry) . P(Dry|Dry) . P(Dry)

                                       = 0.3 x 0.2 x 0.8 x 0.6

                                       = 0.0288

Steps describing the HMM

• Carries set of states: {s1,s2,…sN)
• The process migrates from one state to other, generating a sequence of states as: s_i1,s_i2,….s_ik,…
• Follows the Markov chain rule, where the probability of the current state depends on the previous state.
• In HMM, the states are hidden, but each state randomly generates one of M visible states as {v₁,v₂,….,v_M).
• The following probabilities need to be specified in order to define the Hidden Markov Model, i.e.,

Transition Probabilities Matrices, A =(a_ij), a_ij = P(s_i|s_j)

Observation Probabilities Matrices, B = ((b_i)v_M)), b_i(v_M) = P(v_M|s_i)

A vector of initial probabilities, ?=?i,?i = P(si)

The model is represented by M = (A,B,?)

Example of HMM

Consider the two given states Low, High and two given observations Rain and Dry.

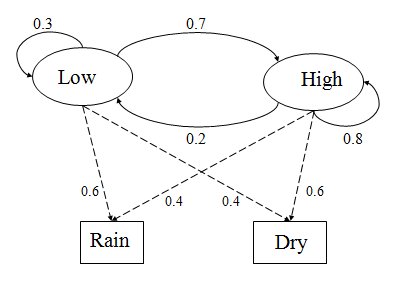
The initial probability for Low and High states be;

P(Low) = 0.4, P(High) = 0.6

The transition probabilities are given as;

P(Low|Low) = 0.3

P(High|Low) = 0.7

P(Low|High) = 0.2

P(High|High) = 0.8

The observation probabilities can be detremined as:

P(Rain|Low) = 0.6

P(Dry|Low) = 0.4

P(Rain|High) = 0.4

P(Dry|High) = 0.3

Now, suppose we want to calculate the probability of a sequence of observations, i.e., {Dry,Rain}

It can be calculated by considering all the hidden state sequences:

P({Dry,Rain}) = P({Dry, Rain}),{Low,Low}) + P(Dry,Rain},{Low,High}) + P({Dry, Rain},{High,Low}) +    P({Dry,Rain},{High,High})

where the first term is:

P({Dry,Rain},{Low,Low}) = P({Dry,Rain}|{Low,Low}) . P({Low,Low})

    = P(Dry|Low) . P(Rain|Low) . P(Low). P(Low|Low)

    = 0.4 x 0.4 x 0.6 x 0.4 x 0.3 

    = 0.01152

Drawbacks of Hidden Markov Model

• Evaluation Problem: A HMM is given, M= (A,B,?), and an observation sequence, O=o1 o2,….oK. Evaluate the probability that model M has generated the sequence O.

• Decoding Problem: A HMM is given, M= (A,B,?), and the observation sequence, O=o1 o2,….oK. Calculate the most likely sequence of hidden states Si which produced this observation sequence O.

• Learning Problem: Given some general structure of HMM and some training observation sequences O=01 o2,….oK. Calculate HMM parameters, M= (A,B,?) which best fits the training data.

Note: Observation O= o1 o2,….oK denotes a sequence of observations oK {v1,……,vM}