Constraint Satisfaction Problems in Artificial Intelligence
Constraint Satisfaction Problems in Artificial Intelligence
We have seen so many techniques like Local search, Adversarial search to solve different problems. The objective of every problem-solving technique is one, i.e., to find a solution to reach the goal. Although, in adversarial search and local search, there were no constraints on the agents while solving the problems and reaching to its solutions.
In this section, we will discuss another type of problem-solving technique known as Constraint satisfaction technique. By the name, it is understood that constraint satisfaction means solving a problem under certain constraints or rules.
Constraint satisfaction is a technique where a problem is solved when its values satisfy certain constraints or rules of the problem. Such type of technique leads to a deeper understanding of the problem structure as well as its complexity.
Constraint satisfaction depends on three components, namely:
- X: It is a set of variables.
- D: It is a set of domains where the variables reside. There is a specific domain for each variable.
- C: It is a set of constraints which are followed by the set of variables.
In constraint satisfaction, domains are the spaces where the variables reside, following the problem specific constraints. These are the three main elements of a constraint satisfaction technique. The constraint value consists of a pair of {scope, rel}. The scope is a tuple of variables which participate in the constraint and rel is a relation which includes a list of values which the variables can take to satisfy the constraints of the problem.
Solving Constraint Satisfaction Problems
The requirements to solve a constraint satisfaction problem (CSP) is:
- A state-space
- The notion of the solution.
A state in state-space is defined by assigning values to some or all variables such as
{X1=v1, X2=v2, and so on…}.
An assignment of values to a variable can be done in three ways:
- Consistent or Legal Assignment: An assignment which does not violate any constraint or rule is called Consistent or legal assignment.
- Complete Assignment: An assignment where every variable is assigned with a value, and the solution to the CSP remains consistent. Such assignment is known as Complete assignment.
- Partial Assignment: An assignment which assigns values to some of the variables only. Such type of assignments are called Partial assignments.
Types of Domains in CSP
There are following two types of domains which are used by the variables :
- Discrete Domain: It is an infinite domain which can have one state for multiple variables. For example, a start state can be allocated infinite times for each variable.
- Finite Domain: It is a finite domain which can have continuous states describing one domain for one specific variable. It is also called a continuous domain.
Constraint Types in CSP
With respect to the variables, basically there are following types of constraints:
- Unary Constraints: It is the simplest type of constraints that restricts the value of a single variable.
- Binary Constraints: It is the constraint type which relates two variables. A value x2 will contain a value which lies between x1 and x3.
- Global Constraints: It is the constraint type which involves an arbitrary number of variables.
Some special types of solution algorithms are used to solve the following types of constraints:
- Linear Constraints: These type of constraints are commonly used in linear programming where each variable containing an integer value exists in linear form only.
- Non-linear Constraints: These type of constraints are used in non-linear programming where each variable (an integer value) exists in a non-linear form.
Note: A special constraint which works in real-world is known as Preference constraint.
Constraint Propagation
In local state-spaces, the choice is only one, i.e., to search for a solution. But in CSP, we have two choices either:
- We can search for a solution or
- We can perform a special type of inference called constraint propagation.
Constraint propagation is a special type of inference which helps in reducing the legal number of values for the variables. The idea behind constraint propagation is local consistency.
In local consistency, variables are treated as nodes, and each binary constraint is treated as an arc in the given problem. There are following local consistencies which are discussed below:
- Node Consistency: A single variable is said to be node consistent if all the values in the variable’s domain satisfy the unary constraints on the variables.
- Arc Consistency: A variable is arc consistent if every value in its domain satisfies the binary constraints of the variables.
- Path Consistency: When the evaluation of a set of two variable with respect to a third variable can be extended over another variable, satisfying all the binary constraints. It is similar to arc consistency.
- k-consistency: This type of consistency is used to define the notion of stronger forms of propagation. Here, we examine the k-consistency of the variables.
CSP Problems
Constraint satisfaction includes those problems which contains some constraints while solving the problem. CSP includes the following problems:
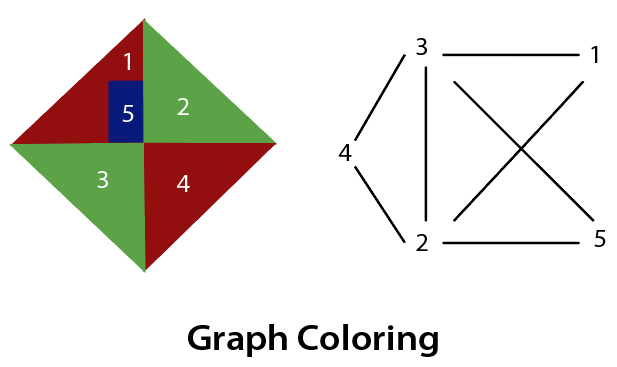
- Graph Coloring: The problem where the constraint is that no adjacent sides can have the same color.
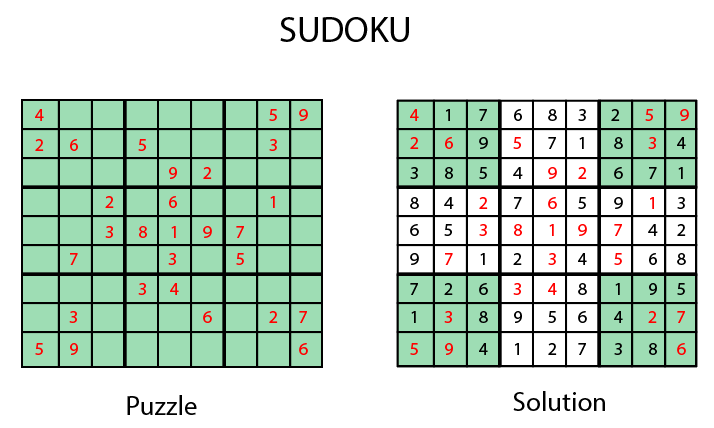
- Sudoku Playing: The gameplay where the constraint is that no number from 0-9 can be repeated in the same row or column.
- n-queen problem: In n-queen problem, the constraint is that no queen should be placed either diagonally, in the same row or column.
Note: The n-queen problem is already discussed in Problem-solving in AI section.
- Crossword: In crossword problem, the constraint is that there should be the correct formation of the words, and it should be meaningful.

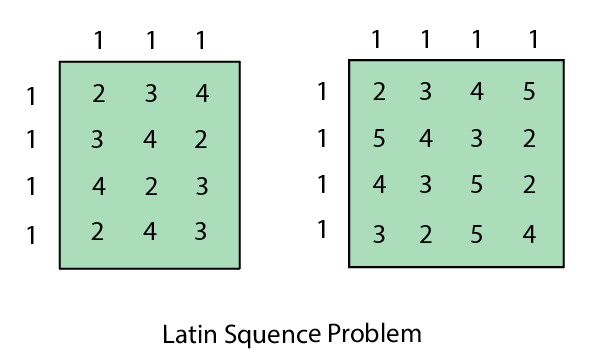
- Latin square Problem: In this game, the task is to search the pattern which is occurring several times in the game. They may be shuffled but will contain the same digits.
- Cryptarithmetic Problem: This problem has one most important constraint that is, we cannot assign a different digit to the same character. All digits should contain a unique alphabet.
Note: We will discuss cryptarithmetic in detail in our next section.