Water Jug Problem in Artificial Intelligence

The Water Jug Problem is a well-known artificial intelligence conundrum that calls for the measurement of a specific amount of water utilizing just two or more jugs of varying sizes. Due to its prominent appearance in the film "Die Hard with a Vengeance," it is often referred to as the "Die Hard Problem." The issue is frequently used in computer science and AI to demonstrate various approaches and algorithms for addressing issues, including breadth-first search, depth-first search, and A* search.

The Brute force process of solving a water jug problem can be shown as:

1. Describe the problem: Decide how many jugs will be used, their capacities, and the volume of water that will be measured.
2. Set up the beginning of the problem: All jugs should be empty to begin with, with the exception of one jug that has the most water possible in it.
3. Define the desired state: Decide how much water has to be measured and which jugs should hold that quantity of water in the finished product.
4. Describe the phases: Determine the feasible course of action, such as filling or emptying a jug, pouring water from one jug to another, or any other restrictions that could be present.
5. Building a search tree: Create a search tree to depict the issue, with each node representing a possible condition for the jugs and each edge representing a potential course of action.
6. Put a search algorithm in place: To identify a path from the starting state to the desired state, pick a suitable search algorithm, such as breadth-first search, depth-first search, or A* search.
7. Once a solution has been developed, it should be evaluated to make sure it is accurate and ideal.

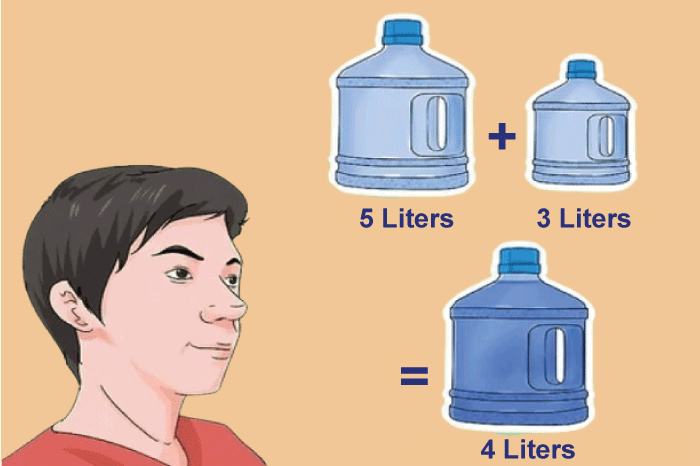
Example 1: You have two jugs with capacities of 5 and 3 liters, for instance. The 3-liter jug is empty, while the 5-liter jug is filled with water. How many liters of water can you accurately measure with these two jugs?

Using the procedures above, the solution is:

Step 1: Using two jugs with capacities of 5 and 3 liters, the first task is to measure 4 liters of water.

Step 2: In the original condition, the 3-liter jug is empty and the 5-liter jug is completely full.

Step 3: The objective is to fill one of the jugs with 4 liters of water.

Step 4: Several options are available.

• Using water from the 5-liter jug, fill the 3-liter container.
• The 3-liter jug of water should be used to fill the 5-liter jug.
• Fill up the 3-liter bottle.
• Empty the 5-liter bottle.
• Fill the 3-liter jug with water by adding it to the 5-liter jug.
• Fill the 5-liter jug with water by adding it to the 3-liter jug.
• Keep in mind that we are unable to pour water from one jug to another if either container is full or empty.

Step 5: This problem's search tree appears as follows:

(5,0) 
 /     \
(2,3)  (0,5)
 |      |
(2,1)  (3,2)
 |      |
(4,0)  (3,0)

The first number on the tree represents the quantity of water in the 5-liter jug, and the second number represents the amount of water in the 3-liter jug, and each node represents a condition of the two jugs. The activities that may be done to change from one state to another are represented by the edges.

Step 6: Starting with the starting state (5,0), we apply the available actions in the following order to solve this issue using depth-first search.

• Fill the 3-liter jug with water by adding water from the 5-liter jug: (2,3) (2,0)
• Fill the 3-liter jug with water by adding it to the 5-liter jug: (0,2)
• Fill the 3-liter jug with water by adding water from the 5-liter jug as follows: (3,2) (3,0)
• Fill the 3-liter jug with water by adding it to the 5-liter jug: (4,0)
• The 5-liter jug now contains 4 liters of water, which is the desired outcome.

Step 7: The answer is accurate and ideal since it takes the fewest steps possible to get at the desired condition.

In conclusion, the Water Jug Problem is a well-known artificial intelligence issue that includes measuring a certain amount of water in two or more jugs of various sizes. By identifying the issue, establishing the starting and desired states, specifying the actions, building a search tree, using a search algorithm, and assessing the answer, the issue may be resolved. Utilizing a suitable search technique, the solution entails employing the available actions to transition from the starting state to the desired one.

Example 2: You have three jugs with sizes of 8, 5, and 3 liters, for instance. The other two jugs are empty, but the 8-liter jug is filled with water. How do you measure 4 litres of water precisely?

The way to use the three jugs with capacities of 8, 5, and 3 litres to precisely measure 4 litres of water.

1. Start with the initial condition (8,0,0), which has the 8-liter jug filled and the other two jugs empty.
2. Fill the 5-liter jug with water by pouring water from the 8-liter jug until the 5-liter jug is full. (3,5,0).
3. The 5-liter jug will contain 2 litres of water once you transfer all of the water from it into the 3-liter jug. (3,2,3).
4. Empty the 3-liter bottle to produce the desired condition. (3,2,0).
5. In order to achieve the state, transfer 2 litres of water from the 5-liter jug into the 3-liter jug, leaving 1 litre of water in the 5-liter jug. (3,3,2).
6. Refill the 5-liter container with water from the 8-liter container, leaving 6 litres of water in the 8-liter container, and the state (6,3,2).
7. Fill the 3-liter jug with water by pouring water from the 5-liter jug, leaving 1 litre of water in the 5-liter jug, producing the following situation. (6,2,3).
8. Empty the 3-liter bottle to produce the desired condition. (6,2,0).
9. The objective state is achieved by transferring 2 litres of water from the 5-liter jug into the 3-liter jug, leaving 4 litres of water-the required amount-in the 5-liter jug. (6,3,1).

In order to get the needed 4 litres in the 5-liter jug, this technique involves a mixture of flowing water between the jugs, emptying the jugs, and filling them back up. In order to identify a solution, we can methodically investigate all potential actions and states by presenting the issue as a search tree.

(8,0,0)
     |
   (3,5,0)
     | 
   (3,2,3)
    /   \
(3,2,0) (3,3,2)
    |     |
(6,2,0) (6,3,2)
    |     |
(6,2,3) (6,3,1)  <-- goal state

The first number in the tree represents the amount of water in the 8-liter jug, the second number represents the amount of water in the 5-liter jug, and the third number represents the amount of water in the 3-liter jug. Each node in the tree represents a condition of the three jugs. The activities that may be done to change from one state to another are represented by the edges.

The different ways of approaching the Water Jug Problem are as follow:

1. Algebraic Method: Equations are used to discover a solution in the Water Jug issue utilising the algebraic approach. The steps are as follows:

Step 1: Define the variables: Let x represent the volume of water in the first jug, y represent the volume in the second jug, and z represent the amount of water that is wanted.

Step 2: Equations to be written down: Using the restrictions of the problem, write out two equations. The entire amount of water in both jugs is determined by the first equation: x + y = a, where a represents the total of the jugs' capacity. The second equation, where m and n are the ratios of the jug capacities, determines how much water is required to produce the desired quantity.

Step 3: Find values for x and y that satisfy both equations by solving the system of equations. Systems of equations can be solved using a variety of techniques, such as substitution or elimination.

Step 4: Verify the answer: Make sure the answer fulfils the requirements of the issue, such as making sure the values of x and y are non-negative and less than or equal to the respective jugs' capacity.

For bigger issue instances, the algebraic technique offers a methodical and effective way to solve the Water Jug problem. However, it necessitates some algebraic understanding and could be more difficult for individuals without a foundation in mathematics.

2. Binary Method: Using binary values to represent the volume of water in each jug, the Water Jug Problem may be solved using the binary approach. The steps are as follows:

Step 1: Establish variables: Let c be the required amount of water, and let a and b represent the first and second jugs' respective capacities.

Step 2: Specify the quantity of water is in each of the jugs: The quantity of water in each jug should be represented using binary values. For instance, if a = 3, you may use the binary numbers 0, 1, 2, or 3 to express how much water is in the first jug. (e.g., 00, 01, 10, 11). Similarly, if b = 5, you may use the binary numbers 0, 1, 2, 3, or 5 to express how much water is in the second jug. (e.g., 000, 001, 010, 011, 100, 101).

Step 3: Filling up the first jug: Set the binary integer that represents the first jug to the highest possible value, such as 11 if a = 3.

Step 4: Water should be moved between the jugs: Transfer water using binary operations from the first jug to the second jug until the second jug has the desired amount of water in it. (c). The binary operations are binary OR, AND, and XOR, as well as bitwise shift (left or right). For instance, to move one unit of water from one jug to another, shift the first jug's binary digits by one (by eliminating the rightmost digit), and then OR the resultant binary number with the digits of the second jug. (Adding the rightmost digit).

Step 5: Verify the answer: Verify that the binary number that results represents the second jug with the appropriate amount of water. (c).

For big issue cases, the binary technique offers a creative and effective solution to the Water Jug problem. It may be constructed using basic bitwise operations without the need for complex mathematical expertise. For people without a background in computer science, it could be challenging to comprehend and use.