Informed Search/ Heuristic Search in AI

An informed search is more efficient than an uninformed search because in informed search, along with the current state information,  some additional information is also present, which make it easy to reach the goal state.

Below we have discussed different types of informed search:

Best-first Search (Greedy search)

A best-first search is a general approach of informed search. Here, a node is selected for expansion based on an evaluation function f(n), where f(n) interprets the cost estimate value. The evaluation function expands that node first, which has the lowest cost. A component of f(n) is h(n) which carries the additional information required for the search algorithm, i.e.,

h(n)= estimated cost of the cheapest path from the current node n to the goal node. 

Note: If the current node n is a goal node, the value of h(n) will be 0.

Best-first search is known as a greedy search because it always tries to explore the node which is nearest to the goal node and selects that path, which gives a quick solution. Thus, it evaluates nodes with the help of the heuristic function, i.e., f(n)=h(n).

Best-first search Algorithm

1. Set an OPEN list and a CLOSE list where the OPEN list contains visited but unexpanded nodes and the CLOSE list contains visited as well as expanded nodes.
2. Initially, traverse the root node and visit its next successor nodes and place them in the OPEN  list in ascending order of their heuristic value.
3. Select the first successor node from the OPEN list with the lowest heuristic value and expand further.
4. Now, rearrange all the remaining unexpanded nodes in the OPEN list and repeat above two steps.
5. If the goal node is reached, terminate the search, else expand further.

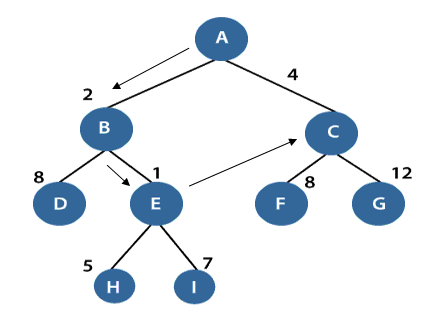
In the above figure, the root node is A, and its next level successor nodes are B and C with h(B)=2 and h(C)=4. Our task is to explore that node which has the lowest h(n) value. So, we will select node B and expand it further to node D and E. Again, search out that node which has the lowest h(n) value and explore it further.

The performance measure of Best-first search Algorithm:

• Completeness: Best-first search is incomplete even in finite state space.
• Optimality: It does not provide an optimal solution.
• Time and Space complexity: It has O(b^m) worst time and space complexity, where m is the maximum depth of the search tree. If the quality of the heuristic function is good, the complexities could be reduced substantially.

Note: Best first searches combines the advantage of BFS and DFS to find the best solution.

Disadvantages of Best-first search

• BFS does not guarantees to reach the goal state.
• Since the best-first search is a greedy approach, it does not give an optimized solution.
• It may cover a long distance in some cases.

A* Search Algorithm

A* search is the most widely used informed search algorithm where a node n is evaluated by combining values of the functions g(n)and h(n). The function g(n) is the path cost from the start/initial node to a node n and h(n) is the estimated cost of the cheapest path from node n to the goal node. Therefore, we have

                                                      f(n)=g(n)+h(n)

where f(n) is the estimated cost of the cheapest solution through n.

So, in order to find the cheapest solution, try to find the lowest values of f(n).

Let’s see the below example to understand better.

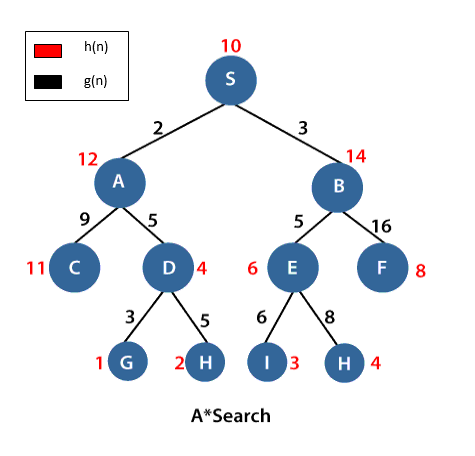
In the above example,  S is the root node, and G is the goal node. Starting from the root node S and moving  towards its next successive nodes A and B. In order to reach the goal node G, calculate the f(n) value of node S, A and B using the evaluation equation i.e.

f(n)=g(n)+h(n)

Calculation of f(n) for node S:

f(S)=(distance from node S to S) + h(S)

• 0+10=10.

Calculation of f(n) for node A:

f(A)=(distance from node S to A)+h(A)

• 2+12=14

Calculation of f(n) for node B:

f(B)=(distance from node S to B)+h(B)

•  3+14=17

Therefore, node A has the lowest f(n) value. Hence, node A will be explored to its next level nodes C and D and again calculate the lowest f(n) value. After calculating, the sequence we get is S->A->D->G with f(n)=13(lowest value).

How to make A* search admissible to get an optimized solution?

A* search finds an optimal solution as it has the admissible heuristic function h(n) which believes that the cost of solving a problem is less than its actual cost. A heuristic function can either underestimate or overestimate the cost required to reach the goal node. But an admissible heuristic function never overestimates the cost value required to reach the goal state. Underestimating the cost value means the cost we assumed in our mind is less than the actual cost. Overestimating the cost value means the cost we assumed is greater than the actual cost, i.e.,

Here, h(n) is the actual heuristic cost value and h’(n) is the estimated heuristic cost value.

Note: An overestimated cost value may or may not lead to an optimized solution, but an underestimated cost value always lead to an optimized solution.

Let’s understand with the help of an example:

Consider the below search tree where the starting/initial node is A and goal node is E. We have different paths to reach the goal node E with their different heuristic costs h(n) and path costs g(n). The actual heuristic cost is h(n)=18. Let’s suppose two different estimation values:

h1'(n)= 12 which is underestimated cost value

h2' (n)= 25 which is overestimated cost value

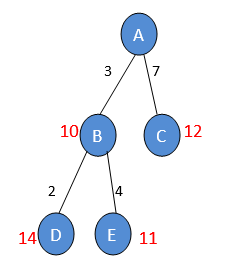
So, when the cost value is overestimated, it will not take any load to search the best optimal path and acquire the first optimal path. But if the h(n) value is underestimated, it will try and reach the best optimal value of h(n) which will lead to a good optimal solution.     

Note: Underestimation of h(n) leads to a better optimal solution instead of overestimating the   value.

The performance measure of A* search

• Completeness: The star(*) in A* search guarantees to reach the goal node.
• Optimality: An underestimated cost will always give an optimal solution.
• Space and time complexity: A* search has O(b^d) space and time complexities.

Disadvantage of A* search

• A* mostly runs out of space for a long period.

AO* search Algorithm

AO* search is a specialized graph based on AND/OR operation. It is a problem decomposition strategy where a problem is decomposed into smaller pieces and solved separately to get a solution required to reach the desired goal. Although A*search and AO* search, both follow best-first search order, but they are dissimilar from one another.

Let's understand AO* working with the help of the below example:

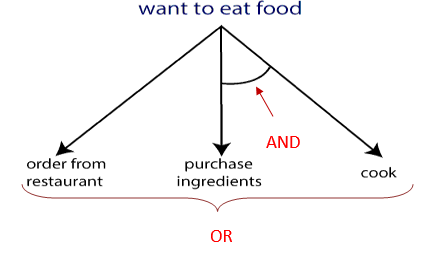
Here, the destination/ goal is to eat some food. We have two ways, either order food from any restaurant or buy some food ingredients and cook to eat food. Thus, we can apply any of the two ways, the choice depends on us. It is not guaranteed whether the order will be delivered on time, food will be tasty or not, etc. But if we will purchase and cook it, we will be more satisfied.

Therefore, the AO* search provides two ways to choose either OR or AND. It is better to choose AND rather OR to get a good optimal solution.

Related Posts:

• Intelligent Agents | Agents in AI
• Artificial Intelligence Tutorial | AI Tutorial
• Alpha-beta Pruning | Artificial Intelligence
• Adversarial Search in Artificial Intelligence
• Hill Climbing Algorithm
• Heuristic Functions in Artificial Intelligence
• Uninformed Search Strategies – Artificial Intelligence
• Inference Rules in Proposition Logic
• Knowledge Based Agents in AI
• Knowledge Representation in AI
• Cryptarithmetic Problem in AI