Logo
×

Local Search Algorithms and Optimization Problem

The informed and uninformed search expands the nodes systematically in two ways:

  • keeping different paths in the memory and
  • selecting the best suitable path,

Which leads to a solution state required to reach the goal node. But beyond these “classical search algorithms," we have some “local search algorithms” where the path cost does not matters, and only focus on solution-state needed to reach the goal node.

A local search algorithm completes its task by traversing on a single current node rather than multiple paths and following the neighbors of that node generally.

Although local search algorithms are not systematic, still they have the following two advantages:

  • Local search algorithms use a very little or constant amount of memory as they operate only on a single path.
  • Most often, they find a reasonable solution in large or infinite state spaces where the classical or systematic algorithms do not work.

Does the local search algorithm work for a pure optimized problem?

Yes, the local search algorithm works for pure optimized problems. A pure optimization problem is one where all the nodes can give a solution. But the target is to find the best state out of all according to the objective function. Unfortunately, the pure optimization problem fails to find high-quality solutions to reach the goal state from the current state.

Note: An objective function is a function whose value is either minimized or maximized in different contexts of the optimization problems. In the case of search algorithms, an objective function can be the path cost for reaching the goal node, etc.

Working of a Local search algorithm

Let's understand the working of a local search algorithm with the help of an example:

Consider the below state-space landscape having both:

  • Location: It is defined by the state.
  • Elevation: It is defined by the value of the objective function or heuristic cost function.
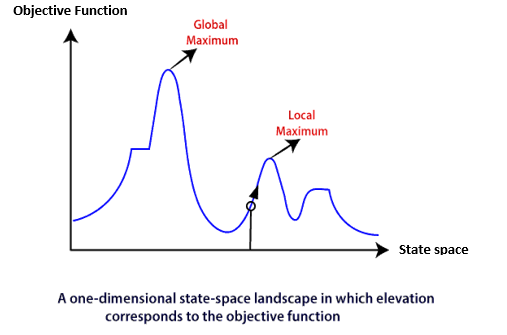
Working of a Local search algorithm

The local search algorithm explores the above landscape by finding the following two points:

  • Global Minimum: If the elevation corresponds to the cost, then the task is to find the lowest valley, which is known as Global Minimum.   
  • Global Maxima: If the elevation corresponds to an objective function, then it finds the highest peak which is called as Global Maxima. It is the highest point in the valley.

We will understand the working of these points better in Hill-climbing search.

Below are some different types of local searches:

  • Hill-climbing Search
  • Simulated Annealing
  • Local Beam Search

We will discuss above searches in the next section.

Note: Local search algorithms do not burden to remember all the nodes in the memory; it operates on complete state-formulation.

Related Topics

Knowledge Based Agents in AI

Knowledge is the basic element for a human brain to know and understand the things logically. When a person becomes knowledgeable about something, he is able to do that thing in a better...

4 minutes read.

5 algorithms that demonstrate artificial intelligence bias

Unfortunately, in the machine learning algorithm, AI bias is the output due to the prejudiced assumption made due to the algorithm development process. AI systems have biases due to the...

3 minutes read.

Gradient Descent

Gradient Descent When training a neural network, an algorithm is used to minimize the loss. This algorithm is called as Gradient Descent. And loss refers to the incorrect outputs given by...

6 minutes read.

Intelligent Agents | Agents in AI

What is an Agent? An agent can be viewed as anything that perceives its environment through sensors and acts upon that environment through actuators. For example, human being perceives their surroundings through...

8 minutes read.

Quantifying Uncertainty

The concept of quantifying uncertainty relies on how an agent can keep away uncertainty with a degree of belief. The term uncertainty refers to that situation or information which is either unknown or...

5 minutes read.

Information Retrieval

Information Retrieval: In order to analyze and categorize the text, we'd like to be able to figure out information about the text, some meaning about the text as well. And,...

14 minutes read.

Hill Climbing Algorithm in AI

Hill Climbing Algorithm: Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of...

4 minutes read.

Theory of First-order Logic

Theory of First-order Logic First-order logic is also called Predicate logic and First-order predicate calculus (FOPL). It is a formal representation of logic in the form of quantifiers. In predicate logic, the input is taken...

4 minutes read.

Hidden Markov Models

Hidden Markov Model is a partially observable model, where the agent partially observes the states. This model is based on the statistical Markov model, where a system being modeled follows the Markov process...

4 minutes read.

Knowledge Representation in AI

In this section, we will understand how to represent the knowledge in the form which could be understood by the knowledge-based agents. The knowledge that is stored in the system is related to...

5 minutes read.

Inference in First-order Logic

Inference in First-order Logic While defining inference, we mean to define effective procedures for answering questions in FOPL. FOPL offers the following inference rules: Inference rules for quantifiersUniversal Instantiation (UI): In this, we can infer any sentence by...

5 minutes read.

Artificial Intelligence vs. Machine learning

Artificial Intelligence This word is trending in the world of technology. Artificial means something which was not present naturally, and it is built by humans, and intelligence means the ability to...

4 minutes read.

Integration of Blockchain and Artificial Intelligence

A Blockchain is a shared database or ledger where pieces of data are stored in data structures known as blocks. So, we can say that Blockchain is the distribution storage...

6 minutes read.

Probabilistic Reasoning

Probabilistic Reasoning Probabilistic Reasoning is the study of building network models which can reason under uncertainty, following the principles of probability theory. Bayesian Networks Bayesian network is a data structure which is used to represent the dependencies among variables....

7 minutes read.

Dynamic Routing

Dynamic Routing Dynamic routing is used to update the routing table and find networks on the routers. It is easier than static routing and default routing, but it is more expensive in terms of...

3 minutes read.

The Wumpus World

The Wumpus world is a game playing which provides an environment to the knowledge-based agent to showcase its stored knowledge. It was developed by Gregory Yob in 1973. About the game:  It...

3 minutes read.

Heuristic Functions in Artificial Intelligence

Heuristic Functions in AI: As we have already seen that an informed search make use of heuristic functions in order to reach the goal node in a more prominent way....

3 minutes read.

Supervised Learning in AI

Supervised Learning in AI Learning Supervised LearningClassification TasksNearest Neighbor ClassificationK nearest neighbor AlgorithmPerceptron LearningSupport Vector MachineRegression TasksLoss FunctionOverfittingRegularizationScikit LearnK Nearest Neighbor ImplementationPerceptron Algorithm ImplementationSupport Vector Machine Algorithm ImplementationRegression Implementation Machine Learning In the Artificial...

33 minutes read.

Forward Chaining in AI : Artificial Intelligence

Forward Chaining is the process which works on the basis of available data to make certain decisions. Forward chaining is the process of chaining data in the forward direction. In forward chaining, we...

4 minutes read.

Neural Networks

Neural Networks are one of the most popular techniques and tools in Machine learning. Neural Networks were inspired by the human brain as early as in the 1940s. Researchers studied the...

5 minutes read.