Probabilistic Reasoning
Probabilistic Reasoning
Probabilistic Reasoning is the study of building network models which can reason under uncertainty, following the principles of probability theory.
Bayesian Networks
Bayesian network is a data structure which is used to represent the dependencies among variables. It is used to represent any full joint distribution. Bayesian networks are also known as belief network, probabilistic network, casual network, and knowledge map.
The representation of networks is done through a directed graph where each node is annotated with quantitative probability information. The graph is a directed acyclic graph. Thus, it has no directed cycles.
The Bayesian networks are based on the following specifications:
- Each node corresponding to a random variable, may be either discrete or continuous. Arrows or a set of links are used to connect a pair of nodes. For example, if there is an arrow from node G to node S, it means G is the parent node of S. Remember, the graph contains no directed cycles as it is an acyclic graph.
- Each node Ai has a conditional probability distribution as P(Ai | Parent(Ai)) that quantifies the effects of parents over the node.
- Set of nodes and the topology of the network specifies the conditional independence relationships which hold in the domain. Conditional independence, when combines with the topology implicitly specify the full joint distribution for all variables.
Example of Bayesian Network
Suppose, Pinku has installed a new burglary alarm. It is reliable to detect a burglary, but it also responds to minor earthquakes. Consider Pinku has two neighbors, Akshat and Aakash who promised Pinku to call him at work when they hear the alarm. Akshat nearly always calls, when any alarm is heard. But sometimes he gets confused with the telephone ringing and the alarm, and calls then, too. Aakash likes loud music and often misses the alarm altogether. In the below figure, we can identify that who has called and who has not. Estimate the probability of a burglary.
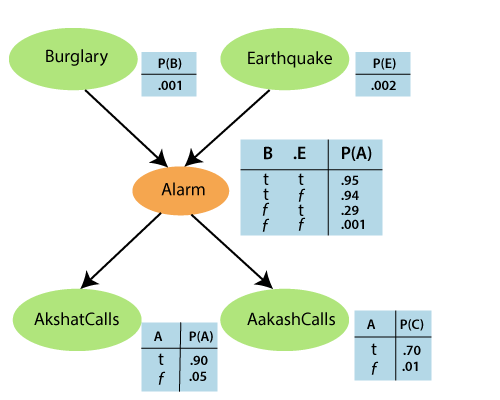
Solution: It is clear from the above graph that earthquake and burglary directly affect the probability of the alarm’s going off. But it is not known that Akshat and Aakash call depends only on the alarm. Hence, the network graph represents the assumption that they did not percieved burglary directly, did not noticed minor earthquakes, and did not confer without calling. The conditional probability table (CPT) shows the conditional distribution. Each row in CPT has a conditional probability of each node value for a conditioning case (a possible combination of the values for parents node). The sum of each row should be 1. In case of a boolean value, the probability of true value is p, and the probability of the false value will be (1-p).
It is seen that no nodes correspond to the fact that Aakash is currently listening to music, or the telephone bell, and confusing Pinku. All these factors get summarized in the uncertainty on the links from Alarm to AkshatCalls and AakashCalls. The probability outlines a potentially infinite set of conditions where the alarm might fail to turn off or both the neighbour’s might fail to call and report it.
So, this shows that a small agent can approximately deal with the large world.
To calculate the probability of Burglary,

Given, P(B)=0.001 and P(A)=0.05(false probability will be taken). We need to calculate P(A|B).
P(A|B)= P(B) x P(E) x 0.95 + P(B) x P(~E) x 0.94 …[P(B)=1]
=1 x 0.002 x 0.95 + 1 x (1-0.002) x 0.94
=0.94
Therefore, probabiliy of Burglary is, P(B|A)=0.94 x 0.001
0.05
= 0.016
Semantics of Bayesian Networks
In order to understand the semantics of the Bayesian networks, there are following two ways used to represent the networks:
- Joint probability distribution
- An encoding of collection of conditional independent statements
Joint Probability Distribution
It is used to understand how the networks are created or constructed. This depends on the network and its semantics to specify the joint distribution over all variables. The notation used for joint distribution probability can be expressed as:
P(x1,…..,xn) =
where parents(Xi) indicates the value of Parents(Xi) which appears in x1, x2,…xn. So, each entry is represented by the product of the appropriate elements of the conditional probability tables in Bayesian networks.
It is proved that are truly the conditional probabilities same as
P(Xi |Parents(Xi)), implied by the joint distribution. So, we can rewrite the above equation as:
P(x1,…..,xn) =
Let’s apply joint probability distribution on the above explained example of Bayesian networks:
Problem: Calculate the probability that the alarm has sounded, but neither an earthquake or burglary occurred, and both Akshat and Aakash made a call to Pinku.
Solution: Given that, both neighbour’s made a call.
Therefore, the joint probability distribution can be calculated by multiplying entries from the joint distribution, i.e.,
P(A,C,a,¬b,¬e) = P(A|a)P(C|a)P(a|¬b ? ¬e)P(¬b)P(¬e)
= 0.90 x 0.70 x 0.001 x 0.999 x 0.998
= 0.000628.
The steps taken to construct the Bayesian network, which gives a good resultant for the joint probability distribution:
- Rewrite all the entries in the joint distribution in terms of the conditional probability by applying the product rule as:
P(x1…..xn) = P(xn|xn-1……,x1).P(xn-1……..,x1).
- Repeat the process and reduce each conjunctive probability to a conditional one with smaller conjunction too. Thus, we get,
P(x1……,xn) = P(xn|xn-1……,x1).P(xn?1 | xn?2,…..,x1)…..P(x2 | x1)P(x1).
= P(xi|xi-1…..,x1)
It is known as the chain rule which holds for any set of random variables.
- On comparing, it is seen that joint distribution specification is equivalent to the general probability assertion, i.e., P(Xi|Xi-1…….,X1) = P(Xi|Parents(Xi))
given that, Parents(Xi) ? (Xi-1……..X1)
- Thus, it is clear that Bayesian network is a correct representation of the domain only when each node is conditionally independent of its other predecessors.
Thus, the methodology used is:
- Nodes: The initial task is to determine the set of variables needed to model the domain. Now, arrange them as {X1…..Xn}.
Note: The sequence can be any. But if it is in the correct sequence always, the resultant will be more effective and compact.
- Links: Apply for loop as:
for i=1 to n do:
Select from X1…….Xi-1 which is a minimal set of parents for Xi.
For each parent, include a link from the parent to Xi.
Pen down the conditional probability tables, P(Xi|Parents(Xi))
So, the parent of node Xi must have all nodes in X1……Xi-1 which directly influences Xi. For example, P(AakashCalls|AkshatCalls,Alarm,Earthquake,Burglary)= P(AakashCalls|Alarm).
Thus, the alarm will be the one and only parent node for AakashCalls. It is because each node is connected to the earlier node resulting into an acyclic network.
Note: It tells a property of the Bayesian network that it does not contain any redundant probability values. Consequently, no inconsistency will occur.
Conditional Independence Statements
For creating conditional independent statements, topological semantics are used. These topological semantics has the following properties:
- These semantics specifies the conditional independence relationships within the graph structure. Further, this helps to derive the numerical semantics.
- The topological semantics specifies that each variable should be conditionally independent of its non-descendents where the parents are given.
- A node is conditionally independent of all the other nodes in a network. Its parents, children, and children’s parents are known. This blanket is known as Markov blanket.
Below figure shows an example of a Markov blanket:
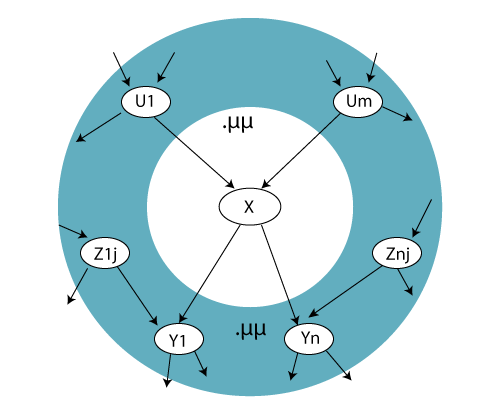
In the above figure, it is shown that a node X is conditionally independent of all other nodes in the Markov blanket network.
To make an efficient representation of the conditional distributions, we use another form of distribution known as Canonical distribution. This distribution is used to handle the worst-case scenario where the relationship between the parents and the child is completely arbitrary. Here, the complete table can be specified by naming the patterns with few parameters.