Propositional Logic

It is a branch of logic which is also known as statement logic, sentential logic, zeroth-order logic, and many more. It works with the propositions and its logical connectivities. It deals with the propositions or statements whose values are true, false, or maybe unknown.

Syntax and Semantics of Propositional Logic

Syntax and semantics define a way to determine the truth value of the sentence.

Syntax: The statements given in a problem are represented via propositional symbols. Each sentence consists of a single propositional symbol. The propositional symbol begins with an uppercase letter and may be followed by some other subscripts or letters. We have two fixed propositional symbols, i.e., True and False.

To convert simple sentences into complex one, following connectives (a connective is used to combine two or more sentences) are used:

• not(¬): It is known as the negation of a sentence. A literal can be a positive literal or a negative literal.
• and(?): When a sentence is having (?) as the main connective. It is known as Conjunction, and its parts are known as Conjuncts. For example, (Y₁ V Y₂) ? (Y₃ V Y₄) ?…(Y_n V Y_m), such type of sentences are known as Conjunctive sentences.
• or(V): When a sentence is having (V) as the main connective. It is known as Disjunction, and its parts are known as Disjuncts. For example, (Y₁ ? Y₂) V (Y₃ ? Y₄) V …(Y_n ? Y_m), such type of sentences are known as Disjunctive sentences.  

• implies(=>): When (Y₁ V Y₂) => Y₃ is given, it is known as the Implication of a sentence. It is like if->then clause, where if this implies then it will happen. Implication is sometimes referred to as Rules or if-then statement. It can also be denoted as (      ) or (       ).
• if and only if (ó): It represents implication at both sides where the expression is (a₁ V a₂)?a_3,. Such type of connective is called biconditional implication. It returns true if both sides satisfy one another, else returns false.This can also be denoted as (?).

Precedence Order of the Connectives

Below table shows the precedence order of the connectives in their decreasing order:

Name	Symbol
Parenthesis/ Brackets	()
Negation/not	¬ or ~
Conjuction/and	?
Disjunction/or	V
Implication	?
Biconditional/ if and only if	ó

Semantics: It defines the rules to determine the truth of a sentence with respect to a specific model. A semantic should be able to compute the truth value of any given sentence.

There are following five rules regarding the semantics of the complex sentences P and Q in a given model m :

¬P: Its value will be false, iff it is true in the model m.

(P ? Q): Its value is true, iff both P and Q are true in m.

(P v Q): Its value is true, iff either P is true, or Q is true in m.

(P=> Q): Its value is true, iff the value of P is false, and that of Q is true in m.

(P ? Q): The value will be true, iff P and Q value is either true or false in the given model m.

Note: Here, iff means if and only if.                    

These five connectives can also be understood with the help of the below described truth table:

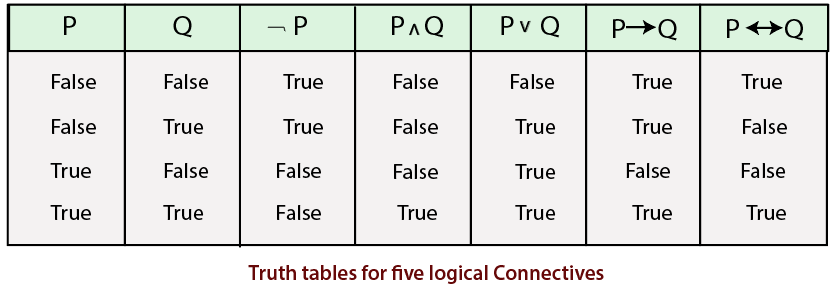
Examples of Propositional Logic

Example 1: Consider the given statement:

If it is humid, then it is raining.

Solution: Let, P and Q be two propositions.

P=It is humid.

Q=It is raining.

It is represented as (P?Q).

Example 2:  It is noon and Ram is sleeping.

Solution: A= It is noon.

B= Ram is sleeping.

It is represented as (A V B).

Example 3: If it is raining, then it is not sunny.

Solution: P= It is raining.

Q= It is sunny.

It is represented as P ? ( ~Q)

Example 4: Ram is a man or a boy.

Solution: X= Ram is a man.

Y= Ram is a boy.

It is represented as (X ? Y).

Example 5: I will go to Delhi if and only if it is not humid.

Solution: A= I will go to Delhi.

B= It is humid.

It is represented as (A ? B).

There can be many examples of Propositional logic.

Propositional Theorem Proving

Theorem proving means to apply rules of inference directly to the sentences.

There are following concepts which are used for theorem proving:

• Logical Equivalence: If the value of P and Q is true in the same set of models, then they are said to be logically equivalence.

Rule Name	Rule
Idempotency Law	(A ? A) = A(AV A) = A
Commutative Law	(A ? B) = (B ? A)(AV B) = (B V A)
De morgan’s Law	~(A ? B) =( ~A V ~B)~(A V B) = (~A ? ~B)
Associative Law	AV(B V C) = (A V B) V CA ?(B ? C) = (A ?B) ? C
Distributive Law	A ?(B V C) = (A ? B) V (A ? C)A V (B ? C) = (A V B) ? (A V C)
Contrapositive Law	A   ? B = ~A    ?   ~B ~A  ?       ~B (Converse of Inverse)
Implication Removal	A    ?   B = ~A V B
Biconditional Removal	A ? B = (A ? B) ? (B  ? A)
Absorption Law	A ? (A V B) ? AAV (A ? B) ?A
Double-negation elimination	~(~A)=A

Table defining the rules used in Propositional logic where A, B, and C represents some arbitrary sentences.

• Validity: If a sentence is valid in all set of models, then it is a valid sentence. Validity is also known as tautology, where it is necessary to have true value for each set of model.
• Satisfiability: If a sentence is true atleast for some set of values, it is a satisfiable sentence.

Let’s understand validity and satisfiability with the help of examples:

Example 1:

(P V Q)    ?   (P ? Q)

P	Q	P V Q	P ? Q	(P V Q)        (P ? Q)
False	False	False	False	True
False	True	True	False	False
True	False	True	False	False
True	True	True	True	True

So, from the above truth table, it is clear that the given expression is satisfiable but not valid.

Example 2:

A	B	A ? B	(A  ? B) ? A	((A ? B) ? A) ? B
False	False	True	False	True
False	True	True	False	True
True	False	False	False	True
True	True	True	True	True

((A  ? B) ? A)  ? B

So, it is clear from the truth table that the given expression is valid as well as satisfiable.

Note: If the given expression is valid, it is by default satisfiable.