Quantifying Uncertainty

The concept of quantifying uncertainty relies on how an agent can keep away uncertainty with a degree of belief. The term uncertainty refers to that situation or information which is either unknown or imperfect.

Earlier, we have seen that the problem-solving agents rely on the belief states (which represents all possible states and generates the future plan) to handle uncertainty. But there were certain drawbacks created when the agent’s program was created:

• Large and complex belief-state representations were created. It was impossible to handle each one of them.
• If the right contingent plan (future plan) is selected, it can grow arbitrarily large.
• There can be a condition sometimes when no plan guarantees to reach the goal. Thus, a method should be there to compare the pros and cons of the plans which are not guaranteed.

Need of Uncertainty

To understand the need, let’s see the below example of uncertain reasoning:

Consider the diagnosis of a cancer patient. By following the propositional logic, a rule can be derived as:

Cancer?age.

But this rule is incorrect as all cancers are not caused due to age effects. There can be other possible causes like environment, genetics, skin type, etc. We can rewrite the rule as:

Cancer?age V  genetics  V skin …

Unfortunately, this rule will also not work because there can be unlimited causes of cancer.

There is only one way to make the rule applicable, i.e., to make it logically exhaustive. But, using logic with such medical like domain fails due to the following reasons:

• Laziness: It is difficult to list all set of antecedents or consequents required to ensure exceptionless rules. With this, it is too typical to use such rules.
• Theoretical Ignorance: There is no complete theory of cancer in the medical science domain.
• Practical Ignorance: Although, we know each rule, but it is uncertain for a specific patient as all tests cannot be run.

Note: Above described points are the demerits of using pure logic

As a result, the agent’s knowledge can only provide a degree of belief. The main tool used to deal with the degree of belief is Probability theory. The term probability theory is that the world is composed of facts which either hold or do not hold in any particular case.

Note: Probability enhances a way to summarize the uncertainty which occurs from the above described reasons, i.e., ignorance and laziness. Thereby solving the quantifying problems.

Decision Theory

Sometimes it is possible that the plan we choose may not be a rational plan. May be there would be a more better option available. Therefore, to make such choices, an agent should have knowledge about:

• Outcomes: It is the result of different states which are completely specified states.
• Preferences: The agent should have preferences between different possible outcomes of several plans.
• Utility Theory: It is used to reason and represent with preferences. The concept of utility theory is that every state has a degree of utility (usefulness) to an agent, and a higher utility state will be preferred to the agent.          

Thus, preferences, when expressed via utilities and combined with probabilities are termed as Decision theory. Hence,

Decision theory = probability theory + utility theory

The principle behind the decision theory is that an agent is rational if and only if it chooses the action which yields the highest expected utility, averaged over all the possible outcomes of the action. This principle is known as the principle of Maximum Expected Utility (MEU).

Basic Probability Notation

Probabilistic assertions define about all possible worlds. The set of all possible worlds is known as the sample space. All the possible worlds are mutually exclusive and exhaustive, i.e., both possible worlds cannot be the case, only one is possible.

A model namely, probability model associates a numerical probability as P() with each possible world. The theory describes that all possible worlds have probability values between 0 and 1. Therefore, the total probability of the sample space is 1.

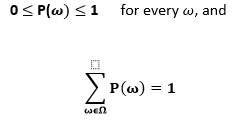
Probabilistic assertions relate to the sets of particularly possible worlds. The sets are always defined via propositions in probability theory. The probability associated with the proposition is defined as the sum of probabilities of the possible worlds, i.e.,

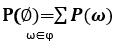
Unconditional Probabilities

The probability which refers to the degrees of belief in propositions when no other information is available. It is also known as Prior probabilities (priors).

For example, the probability of rolling a fair dice is:

P(total=11) = P(5,6) +P(6,5)

                   = 1/36 + 1/36

                  = 1/18.      

Here, the P(total=11) is known as the prior or unconditional probability.

Therefore, an unconditional probability is the independent chance of occurrence of a single outcome from a set of all possible outcomes.

Conditional Probabilities

It is the probability of an event where it is given that an event has already occurred. Conditional probability is also known as Posterior probabilities (posterior).

For example, it is given that the probability of the person having fever is 5% only. Thus, the conditional probability is higher than 75% of those persons who are currently suffering from fever.

Mathematically, a conditional probability is derived in terms of unconditional probability for any propositions x and y.

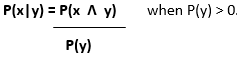
The above rule can also be described in another form known as the Product rule.

Mathematically, it is represented as;

P(x ? y) = P(x|y) . P(y)

The product rule is based on the fact that, for every x and y to be true, value of y should be true. Also, the value of x should be true for a given value of y.

Language of propositions

There are following terms used to represent the propositions:

• Factored representation: It is the representation of a possible world via a set of variable or value pairs.
• Random variables: The variables used in the probability theory are known as random variables.
• Domain: It is a set of all the possible values. Every random variable has a domain.
• Probability Distribution: It is the bold P used to indicate the result for the random variables.
• Probability density function (pdfs): This function enables a way to measure the sets of all possible worlds.
• Full joint probability distribution: It derives the probability of the assignment of every completed value to the random variables.
• Absolute Independence: It occurs between the subsets of the random variables. It allows the full joint distribution of the values factored into its smaller joint distributions.