2D Rotation

The Rotation of any object depends upon the two points.

Rotation Point: It is also called the Pivot point.

Rotation Angle: It is denoted by Theta ().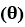

We can rotate an object in two ways-

Clockwise: An object rotates clockwise if the value of the Rotation angle is negative (-).

Anti-Clockwise: An object rotates anti-clockwise if the value of the Rotation angle is positive (+).

We can apply Rotation on following objects-

• Straight Lines
• Curved Lines
• Polygon
• Circle

For Example-

Rotation of a Point: If we want to Rotate a point A (P₀, Q₀) that has a Rotation angle 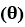with distance r from origin to A` (P₁, Q₁) that has a Rotation angle 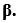. Then, we can rotate by following Rotation equation-

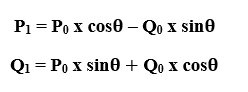
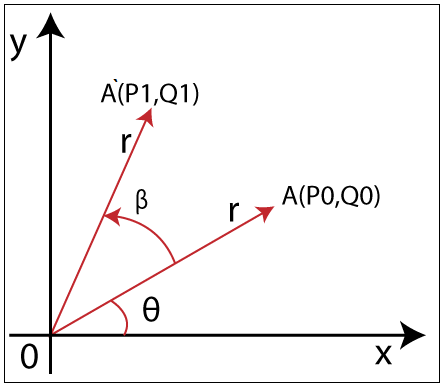
We can represent the coordinates of point A (P₀, Q₀) by using standard trigonometry-

We can also define point A` (P₁, Q₁) in the same way-

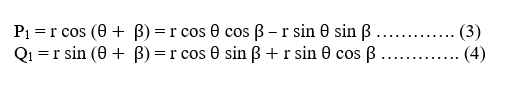
By using equation (1) (2) (3) (4), we will get-

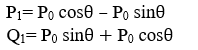
We can also represent the Rotation in the form of matrix-

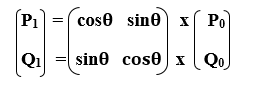
Homogeneous Coordinates Representation: The Rotation can also be represented in the form of 3 x 3 Rotation matrix-

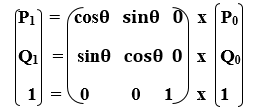
Example- A line segment with the starting point (0, 0) and ending points (5, 5). Apply 30-degree rotation anticlockwise direction on the line. Find the new coordinates of the line?

Solution- We can rotate the straight line by its endpoints with the same angle.

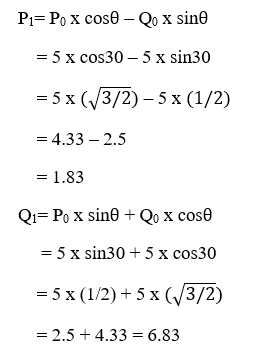
We have,

(P₀, Q₀) = (0, 0)

Rotation Angle () = 30°

Let the new coordinates of line = (P₁, Q₁)

We can apply the rotation matrix, then,

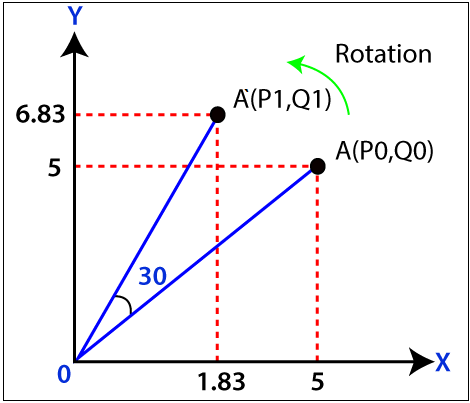
Thus, the new endpoint coordinates of the line are = (P₁, Q₁) = (1.83, 6.83)