Computer Graphics Window

“The process of selecting and viewing an image with different views, called windowing.”

All the objects in the real world have a size. We can measure the size and location of an object by the unit.

For Example-We use the meter unit to measure both size and the location of the object.  

When we represent the image of an object on the screen, then we use the screen coordinate system. The screen coordinate system is used to define the location of the object. When we select the screen coordinate system, then the image can be displayed on the screen.

“The Capability to show some part of an object in a window is known as windowing.”

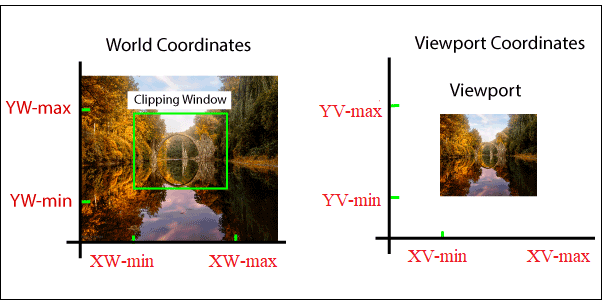
“The rectangular area describes in the world coordinate system is called the window.”

Viewport:

“The viewport can be defined as an area on the screen which is used to display the object.” The window is an area space for the object. Viewport surrounds the object. We need the coordinate transformation to display the object on the screen. We can define many viewports on a different area of the screen and also see the same object from a different angle in the viewport.

Window to Viewport transformation:

“Window to viewport transformation is a process of converting two-dimensional or world into a device coordinate.”

The object inside the clipping window is mapped to the viewport. The viewport is displayed inside the interface window on the screen. We can use the clipping window to select the part of an object, and the viewport is used to display the selected part of the object on the screen or output device.

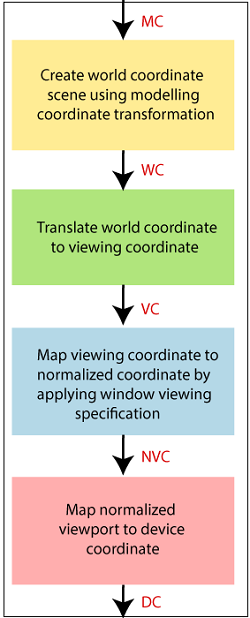
• Steps for Window to Viewport Transformation: We can follow the following steps for transform window to viewport:

Step 1: Translation of the window towards the Origin- If we shift the window towards the origin, the upper left, and the lower-left corner of the window will be negative (-). The translation factor also should be negative (-).

Step 2: Resize the window to viewport size- To Convert the size of the window into the size of the viewport, we will use the following formulas:

 S_{x =}   XV_max – XV_min / XW_max – XW_min

 S_{y =}   YV_max – YV_min / YW_max – YW_min

Step 3: Translation of window (Position of window and viewport must be same)- If the lower-left corner of viewport is (0, 0), then the window lower-left corner is already shifted on origin after following step 1.

If the lower-left corner is not equal to (0, 0), then the translation factor should be positive (+).

It may be possible that sometimes the size of viewport is greater or smaller than the window. In that situation, we have to enlarge or compress the size of the window according to the viewport. We can perform it using some mathematical calculations.

A point on window = (XW, YW)

Corresponding point on viewport = (XV, YV)

• To calculate (XV, YV) –

Normalized point on window = (XW- XW_min / XW_max - XW_min)

                                                    (YW- YW_min / YW_max - YW_min)

Normalized point on viewport = (XV- XV_min / XV_max - XV_min)

                                                     (YV- YV_min / YV_max - YV_min)

• Now, the position of object in viewport and window are same-

For Coordinate x:

(XW- XW_min / XW_max - XW_min) = (XV- XV_min / XV_max - XV_min)

For Coordinate y:

(YW- YW_min / YW_max - YW_min) = (YV- YV_min / YV_max - YV_min)

Now, we get

XV = XV_min + (XW- XW­_min) S_x

YV = YV_min + (YW- YW­_min) S_y

Here S_x and S_y are the scaling factor for x and y coordinate.

  S_{x =}   XV_max – XV_min / XW_max – XW_min

 S_{y =}   YV_max – YV_min / YW_max – YW_min

Some Important Points:

1. We can select the world coordinate system according to the application program.
2. We can select the screen coordinate system according to the desired design.
3. Viewing transformation is a connection between the world and the screen coordinates.

Advantages:

We can easily represent images on the display screen according to the user’s needs.

Related Posts:

• Bresenham’s Line Drawing Algorithm in Computer Graphics
• Mid-Point Line Drawing Algorithm in Computer Graphics
• Pointing and Positioning Technique Computer Graphics
• Scan Conversion of an Ellipse Computer Graphics
• Bresenham’s Circle Drawing Algorithm in Computer Graphics
• DDA line Drawing Algorithm in Computer Graphics
• Polygon Clipping in Computer Graphics
• Line Clipping in Computer Graphics
• Clipping in Computer Graphics
• 3D Rotation in Computer Graphics
• Input Devices in Computer Graphics