DDA line Drawing Algorithm in Computer Graphics
DDA (Digital Differential Analyzer) Line Drawing Algorithm
The Digital Differential Analyzer helps us to interpolate the variables on an interval from one point to another point. We can use the digital Differential Analyzer algorithm to perform rasterization on polygons, lines, and triangles.
Digital Differential Analyzer algorithm is also known as an incremental method of scan conversion. In this algorithm, we can perform the calculation in a step by step manner. We use the previous step result in the next step.
As we know the general equation of the straight line is:
y = mx + c
Here, m is the slope of (x1, y1) and (x2, y2).
m = (y2 – y1)/ (x2 – x1)
Now, we consider one point (xk, yk) and (xk+1, yk+1) as the next point.
Then the slope m = (yk+1 - yk)/ (xk+1 - xk)
Now, we have to find the slope between the starting point and ending point. There can be following three cases to discuss:
Case 1: If m < 1
Then x coordinate tends to the Unit interval.
xk+1 = xk + 1
yk+1 = yk + m
Case 2: If m > 1
Then y coordinate tends to the Unit interval.
yk+1 = yk + 1
xk+1 = xk + 1/m
Case 3: If m = 1
Then x and y coordinate tend to the Unit interval.
xk+1 = xk + 1
yk+1 = yk + 1
We can calculate all intermediate points with the help of above three discussed cases.
Algorithm of Digital Differential Analyzer (DDA) Line Drawing
Step 1: Start.
Step 2: We consider Starting point as (x1, y1), and ending point (x2, y2).
Step 3: Now, we have to calculate ?x and ?y.
?x = x2-x1
?y = y2-y1
m = ?y/?x
Step 4: Now, we calculate three cases.
If m < 1
Then x change in Unit Interval
y moves with deviation
(xk+1, yk+1) = (xk+1, yk+1)
If m > 1
Then x moves with deviation
y change in Unit Interval
(xk+1, yk+1) = (xk+1/m, yk+1/m)
If m = 1
Then x moves in Unit Interval
y moves in Unit Interval
(xk+1, yk+1) = (xk+1, yk+1)
Step 5: We will repeat step 4 until we find the ending point of the line.
Step 6: Stop.
Example: A line has a starting point (1,7) and ending point (11,17). Apply the Digital Differential Analyzer algorithm to plot a line.
Solution: We have two coordinates,
Starting Point = (x1, y1) = (1,7)
Ending Point = (x2, y2) = (11,17)
Step 1: First, we calculate ?x, ?y and m.
?x = x2 – x1 = 11-1 = 10
?y = y2 – y1 = 17-7 = 10
m = ?y/?x = 10/10 = 1
Step 2: Now, we calculate the number of steps.
?x = ?y = 10
Then, the number of steps = 10
Step 3: Weget m = 1, Third case is satisfied.
Now move to next step.
| xk | yk | xk+1 | yk+1 | (xk+1, yk+1) |
| 1 | 7 | 2 | 8 | (2, 8) |
| 3 | 9 | (3, 9) | ||
| 4 | 10 | (4, 10) | ||
| 5 | 11 | (5, 11) | ||
| 6 | 12 | (6, 12) | ||
| 7 | 13 | (7, 13) | ||
| 8 | 14 | (8, 14) | ||
| 9 | 15 | (9, 15) | ||
| 10 | 16 | (10, 16) | ||
| 11 | 17 | (11, 17) |
Step 4: We will repeat step 3 until we get the endpoints of the line.
Step 5: Stop.
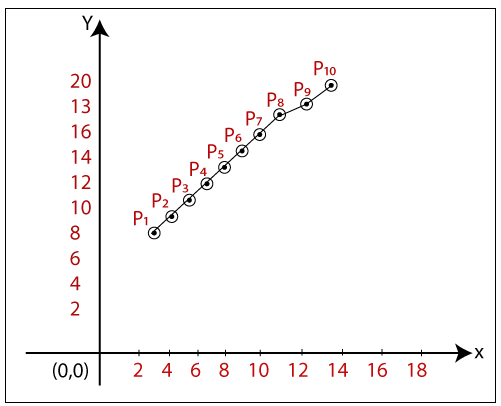
The coordinates of drawn line are-
P1 = (2, 8)
P2 = (3, 9)
P3 = (4, 10)
P4 = (5, 11)
P5 = (6, 12)
P6 = (7, 13)
P7 = (8, 14)
P8 = (9, 15)
P9 = (10, 16)
P10 = (11, 17)
Advantages of Digital Differential Analyzer
- It is a simple algorithm to implement.
- It is a faster algorithm than the direct line equation.
- We cannot use the multiplication method in Digital Differential Analyzer.
- Digital Differential Analyzer algorithm tells us about the overflow of the point when the point changes its location.
Disadvantages of Digital Differential Analyzer
- The floating-point arithmetic implementation of the Digital Differential Analyzer is time-consuming.
- The method of round-off is also time-consuming.
- Sometimes the point position is not accurate.
Related Posts:
- Midpoint Circle Drawing Algorithm in Computer Graphics
- Mid-Point Line Drawing Algorithm in Computer Graphics
- Bresenham’s Line Drawing Algorithm in Computer Graphics
- Bresenham’s Circle Drawing Algorithm in Computer Graphics
- Line Drawing Algorithm in Computer Graphics
- Line Clipping in Computer Graphics
- Computer Graphics Tutorial
- Input Devices in Computer Graphics
- Animation in Computer Graphics
- Output Devices in Computer Graphics