2D Scaling

In scaling, we can expend or compress the size of any object. We can apply scaling on the object by multiplying the original coordinates with scaling factors.

The term scaling factor is used to define whether the size of an object is increased or decreased. We can represent the scaling factor by ‘Sx’ for the x- axis and ‘Sy’ for the y-axis.

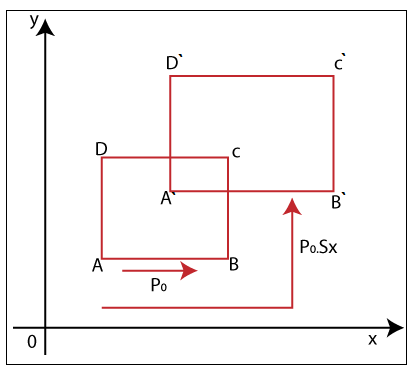
For Example- If we want to scale an object that has R (P₀, Q₀) coordinate and the new coordinates of an object are R` (P₁, Q₁) then the equation will be-

P₁ = P₀. S_x

Q₁ = Q₀. S_y

We can also represent Scaling in the form of Matrix-

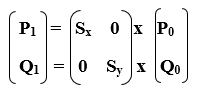
Homogeneous Coordinates Representation: The scaling is also represented in the form of 3 x 3 matrix-

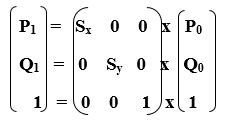
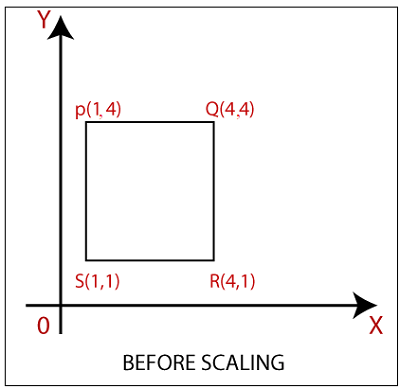
Example: A Square object with the coordinate points P (1, 4), Q (4, 4), R (4, 1), T (1,1). Apply the scaling factor 3 on the X-axis and 4 on the Y-axis. Find out the new coordinates of the square?

Solution: We have,

Coordinates Points for Square = P (1, 4), Q (4, 4), R (4, 1), S (1, 1)

Scaling factor along with X axis (Sx) = 3

Scaling factor along with Y axis (Sy)= 4

Applying the equation to find the new coordinates-

For Coordinate P (1, 4)-

Let the new Coordinate for P = (P₁, Q₁)

P₁ = P₀. Sx = 1 x 3 = 3

Q₁ = Q₀. Sy = 4 x 4 = 16

The new Coordinates = (3, 16)

For Coordinate Q (4, 4)-

Let the new Coordinate for Q = (P,₁ Q₁)

P₁ = P₀. Sx = 4 x 3 = 12

Q₁ = Q₀. Sy = 4 x 4 = 16

The new Coordinates = (12, 16)

For Coordinate R (4, 1)-

Let the new Coordinate for R = (P₁, Q₁)

P₁ = P₀. Sx = 4 x 3 = 12

Q₁ = Q₀. Sy = 1 x 4 = 4

The new Coordinates = (12, 4)

For Coordinate S (1, 1)-

Let the new Coordinate for S = (P₁, Q₁)

P₁ = P₀. Sx = 1 x 3 = 3

Q₁ = Q₀. Sy = 1 x 4 = 4

The new Coordinates = (3, 4)

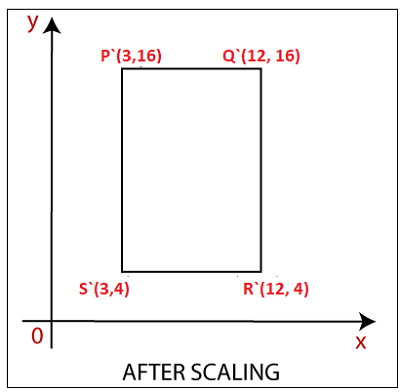
Thus, the new coordinates for square after scaling = P (3, 16), Q (12, 16), R (12, 4), S (3, 4).