3D Reflection

The Reflection is a mirror image of the original object. We can differentiate 2D and 3D reflection by adding Z-axis. The Z-axis shows the depth of the surface. In the Reflection process, the size of the object does not change.

We can represent Reflection by using the following three ways-

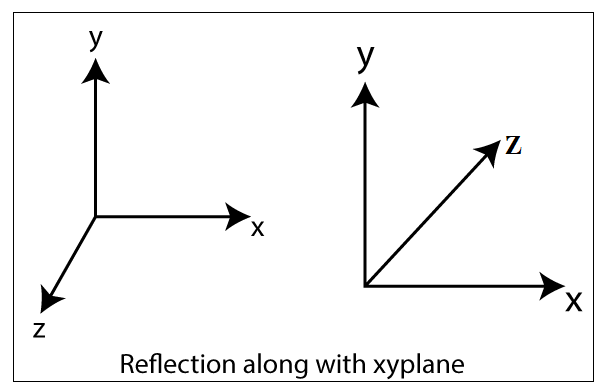
• Reflection along with xy Plane: In the xy plane reflection, the value of z is negative.

x₁ = x₀

y₁ = y₀

z₁ = -z₀

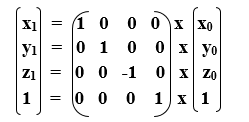
Matrix of 3D Reflection-

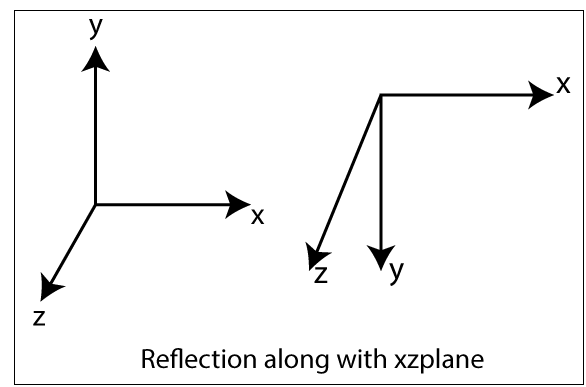
• Reflection along with xz Plane: In the xz plane reflection the value of y is negative.

x₁ = x₀

y₁ = -y₀

z₁ = z₀

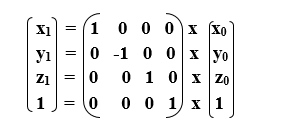
Matrix of 3D Reflection-

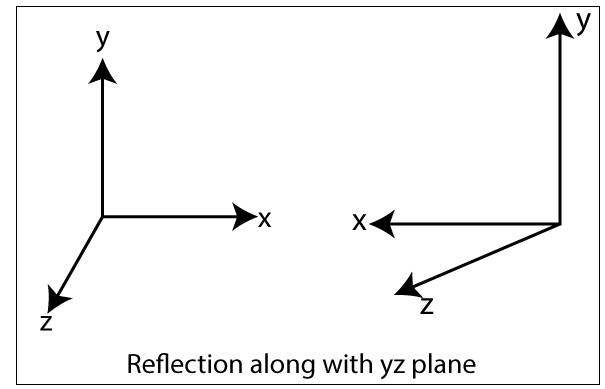
• Reflection along with yz Plane: In the yz plane reflection the value of x is negative.

x₁ = -x₀

y₁ = y₀

z₁ = z₀

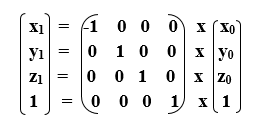
Matrix of 3D Reflection-

Example: A 3D triangle with coordinates points P (4, 5, 2), Q (7, 5, 3), R (6, 7, 4). Apply reflection on xy plane and find the new coordinates of triangle?

Solution: We have,

The initial coordinates of triangle = P (4, 5, 2), Q (7, 5, 3), R (6, 7, 4)

Reflection Plane = xy

Let the new coordinates of triangle = (x₁, y₁, z)

For Coordinate P (4, 5, 2)-

X₁ = x₀ = 4

y₁ = y₀ = 5

z₁ = -z₀= -2

The new coordinates = (4, 5, -2)

For Coordinate Q (7, 5, 3)-

X₁ = x₀ = 7

Y₁ = y₀ = 5

Z₁ = -z₀= -3

The new coordinates = (7, 5, -3)

For Coordinate P (6, 7, 4)-

X₁ = x₀ = 6

y₁ = y₀ = 7

z₁ = -z₀= -4

The new coordinates = (6, 7, 4)