3D Rotation

The 3D rotation is different from 2D rotation. In 3D Rotation we also have to define the angle of Rotation with the axis of Rotation.

For Example- Let us assume,

The initial coordinates of an object = (x₀, y₀, z₀)

The Initial angle from origin = β

The Rotation angle = θ

The new coordinates after Rotation = (x₁, y₁, z₁)

In Three-dimensional plane we can define Rotation by following three ways-

• X-axis Rotation: We can rotate the object along x-axis. We can rotate an object by using following equation-

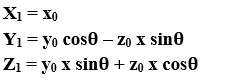
We can represent 3D rotation in the form of matrix-

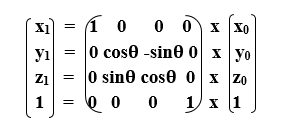
• Y-axis Rotation: We can rotate the object along y-axis. We can rotate an object by using following equation-

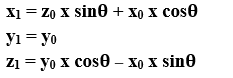
We can represent 3D rotation in the form of matrix-

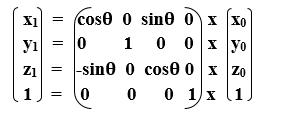
• Z-axis Rotation: We can rotate the object along z-axis. We can rotate an object by using following equation-

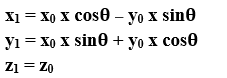
We can represent 3D rotation in the form of matrix-

Example: A Point has coordinates P (2, 3, 4) in x, y, z-direction. The Rotation angle is 90 degrees. Apply the rotation in x, y, z direction, and find out the new coordinates of the point?

Solution: The initial coordinates of point = P (x₀, y₀, z₀) = (2, 3, 4)

Rotation angle (θ) = 90°

For x-axis-

Let the new coordinates = (x₁, y₁, z₁) then,

x₁= x₀ = 2

y₁= y₀ x cosθ – z₀ x sinθ = 3 x cos90°– 4 x sin90° = 3 x 0 – 4 x 1 = -4

z₁= y₀ x sinθ + z₀ x cosθ = 3 x sin90°+ 4 x cos90° = 3 x 1 + 4 x 0 = 3

The new coordinates of point = (2, -4, 3)

For y-axis-

Let the new coordinates = (x₁, y₁, z₁) then,

X₁= z₀ x sinθ + x₀ x cosθ = 4 x sin90° + 2 x cos90° = 4 x 1 + 2 x 0 = 4

y₁= y₀ = 3

z₁= y₀ x cosθ – x₀ x sinθ = 3 x cos90°– 2 x sin90° = 3 x 0 – 4 x 0 = 0

The new coordinates of point = (4, 3, 0)

For z-axis-

Let the new coordinates = (x₁, y₁, z₁) then,

x₁= x₀ x cosθ – y₀ x sinθ = 2 x cos90° – 3 x sin90° = 2 x 0 + 3 x 1 = 3

y₁= x₀ x sinθ + y₀ x cosθ = 2 x sin90° _­+ 3 x cos90° = 2 x 1 + 3 x 0 = 2

z₁= z₀ =4

The New Coordinates of points = (3, 2, 4)