3d Scaling

The 2D and 3D scaling are similar, but the key difference is that the 3D plane also includes the z-axis along with the x and y-axis.

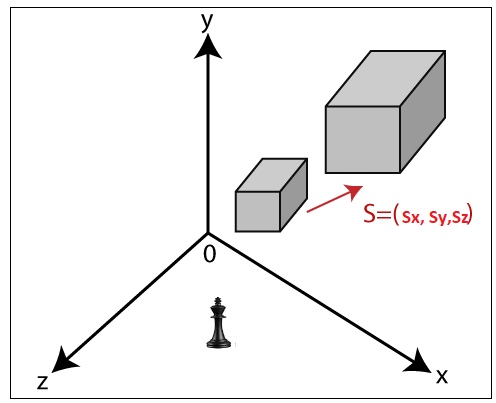
In scaling, we can expend or compress the size of any object. We can apply scaling on the object by multiplying the original coordinates with scaling factors.

The term scaling factor is used to define whether the size of the object is increased or decreased. We can represent the scaling factor by ‘S_x’ for the x-axis, ‘S_y’ for the y-axis, and ‘S_z’ for the z-axis.

The increment and decrement of an object is depends on two conditions. They are-

If scaling factor (S_x, S_y, S_z) > 1, then the size of the object increased.

If scaling factor (S_x, S_y, S_z) < 1, then the size of the object decreased.

For Example: Let us assume,

The initial coordinates of object = P (x₀, y₀, z₀)

Scaling factor for x-axis = S_x

Scaling factor for y-axis = S_y

Scaling factor for z-axis = S_z

The coordinates after Scaling = Q (x₁, y₁, z₁)

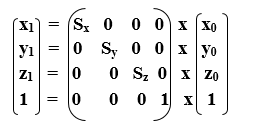
We can represent the 3D Scaling in the form of equation-

X₁ = x₀. S_x

Y₁ = y₀. S_y

Z₁ = z₀. S_z

Matrix representation of 3D Scaling-

Example: A 3D object that have coordinates points P(1, 4, 4), Q(4, 4, 6), R(4, 1, 2), T(1, 1, 1) and the scaling parameters are 3 along with x-axis, 4 along with y-axis and 4 along with z-axis. Apply scaling to find the new coordinates od the object?

Solution: we have,

The initial coordinates of object = P (1, 4, 4), Q (4, 4, 6), R (4, 1, 2), S (1, 1, 1)

Scaling factor along with x-axis (S_x) = 3

Scaling factor along with y-axis (S_y) = 4

Scaling factor along with z-axis (S_z) = 4

Let the new coordinates after scaling = (x₁, y₁, z₁)

For coordinate P-

x₁ = x₀ x S_x = 1 x 3 = 3

y₁ = y₀ x S_y = 4 x 4 = 16

z₁ = z₀ x S_z = 4 x 4 = 16

The new coordinates = (3, 16, 16)

For coordinate Q-

x₁ = x₀ x S_x = 4 x 3 = 12

y₁ = y₀ x S_y = 4 x 4 = 16

z₁ = z₀ x S_z = 6 x 4 = 24

The new coordinates = (12, 16, 24)

For coordinate R-

x₁ = x₀ x S_x = 4 x 3 = 12

y₁ = y₀ x S_y = 1 x 4 = 4

z₁ = z₀ x S_z = 2 x 4 = 8

The new coordinates = (12, 4, 8)

For coordinate S-

x₁ = x₀ x S_x = 1 x 3 = 3

y₁ = y₀ x S_y = 1 x 4 = 4

z₁ = z₀ x S_z = 1 x 4 = 4

The new coordinates = (3, 4, 4)

Thus, the new coordinates after scaling = P (3, 16, 16), Q (12, 16, 24), R (12, 4, 8), S (3, 4, 4).