3D Translation

A 3D Translation process contains the x-axis, y-axis, and z-axis. We can move any object from one place to another without changing the shape of the object.

For Example-
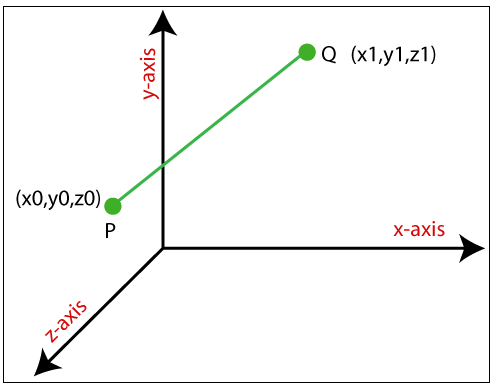
Translation of a Point: If we want to translate a point from P (x₀, y₀, z₀) to Q (x₁, y₁, z₁), then we have to add Translation coordinates (T_x, T_y, T_z) with original coordinates.

We can also represent the 3D Translation in matrix form-

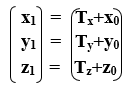
We can apply Translation on the following objects-

• Line
• Rectangle
• Polygon
• Square

3D Translation Matrix Representation:

The above Translation is also shown in the form of 3 x 3 matrix-

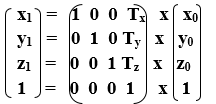
Here Translation coordinates (T_x, T_y, T_z) are also called “Translation or Shift Vector.”

Example: A Point has coordinates P (1, 2, 3) in x, y, z-direction. Apply the translation with a distance of 2 towards x-axis, 3 towards y-axis, and 4 towards the z-axis. Find the new coordinates of the point?

Solution: We have,

Point P = (x₀, y₀, z₀) = (1,2,3)

Shift Vector = (T_x, T_y, T_z)

Let us assume the new coordinates of P = (x₁, y₁, z₁)

Now we are going to add translation vector and given coordinates, then

X₁ = x₀ + T_x = (1 + 2) = 3

Y₁ = y₀ + T_y = (2 + 3) = 5

Z₁ = z₀ + T_z = (3 + 4) = 7

Thus, the new coordinates are = (3, 5, 7)