Logo

Bresenham’s Line Drawing Algorithm in Computer Graphics

This algorithm was introduced by “Jack Elton Bresenham” in 1962. This algorithm helps us to perform scan conversion of a line. It is a powerful, useful, and accurate method. We use incremental integer calculations to draw a line. The integer calculations include addition, subtraction, and multiplication.

In Bresenham’s Line Drawing algorithm, we have to calculate the slope (m) between the starting point and the ending point.

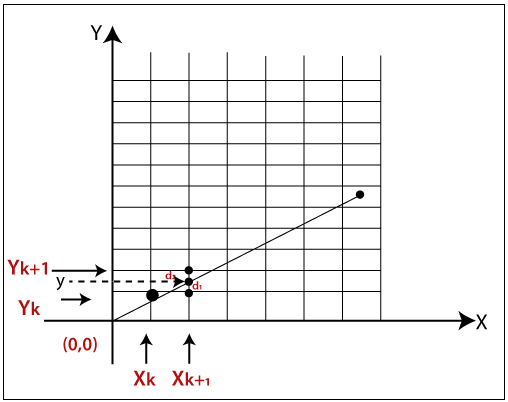
Bresenham’s Line Drawing Algorithm

As shown in the above figure let, we have initial coordinates of a line = (xk, yk)

The next coordinates of a line = (xk+1, yk+1)

The intersection point between yk and yk+1 = y

Let we assume that the distance between y and yk = d1

The distance between y and yk+1 = d2

Now, we have to decide which point is nearest to the intersection point.                             

If m < 1

    then x = xk+1    { Unit Interval}

                      y = yk+1   { Unit Interval}                     

As we know the equation of a line-

y = mx +b

Now we put the value of x into the line equation, then

y = m(xk+1) +b                 …………. (1)

The value of d1 = y - yk

Now we put the value of d1 in equation (1).

y = m (xk+1) +b - yk

Now, we again put the value of y in the previous equation then we got,

d2 = yk+1 – y

    = yk + 1 – m (xk+1) – b

Now, we calculate the difference between d1 – d2

If d1 < d2

Then yk+1 = yk                         {we will choose the lower pixel as shown in figure}  

If d1 => d2

Then yk+1 = yk+1                     {we will choose the upper pixel as shown in figure}

Now, we calculate the values of d1 - d2

(d1 - d2)= m (xk+1) +b - yk - yk - 1 + m (xk+1) + b

We simplified the above equation and replaced the m with ?y/?x.

(d1 - d2) = 2 m (xk+1) -2yk + 2b-1

We multiplied ?x at both side then we got,

?x (d1 - d2) = ?x (2m (xk+1) -2yk + 2b-1)

We consider ?x (d1 - d2) as a decision parameter (P­k), so

pk = ?x (d1 - d2)

After calculation we got,

Pk = 2?yxk + 2?y - 2?xyk +?x (2b-1)

Then, the next coordinate of pk

pk+1 = 2?yxk+1 + 2?y - 2?xyk+1 +?x (2b-1)

 Now, the difference between pk+1 – pk then,

pk+1 – pk = 2?y (xk+1-xk) – 2?x (yk+1-yk)

pk+1 = pk + 2?y (xk+1-xk) – 2?x (yk+1-yk)        {Decision parameter coordinate}

Now, we put the value of xk+1 in above equation then we got,

 pk+1 = pk + 2?y – 2?x (yk+1 - yk)         {New decision parameter when m <1}    

Similarly, if m >1, the new decision parameter for next coordinate will be

pk+1 = pk + 2?y – 2?x (xk+1 - xk)          {New decision parameter when m >1}

If pk >= 0                                                 {For coordinate y}

Then,

yk+1 = yk+1                                                {We will choose the nearest yk+1 pixel}

The next coordinate will be (xk+1, yk+1)

If pk < 0

Then,

yk+1 = yk                                                                                 {We will choose the nearest yk pixel}

The next coordinate will be (xk+1, yk)

Similarly,

If pk >= 0                                                   {For coordinate x}

Then,

xk+1 = xk+1                                                 {We will choose the nearest xk+1 pixel}

The next coordinate will be (xk+1, yk+1)

If pk < 0

Then,

xk+1 = xk                                                                               {We will choose the nearest xk pixel}

The next coordinate will be (xk, yk+1)

Algorithm of Bresenham’s Line Drawing Algorithm

Step 1: Start.

Step 2: Now, we consider Starting point as (x1, y1) and endingpoint (x2, y2).

Step 3: Now, we have to calculate ?x and ?y.

              ?x = x2-x1

                    ?y = y2-y1

              m = ?y/?x               

Step 4: Now, we will calculate the decision parameter pk with following formula.

                       pk = 2?y-?x

Step 5: Theinitial coordinates of the line are (xk, yk), and the next coordinatesare (xk+1, yk+1). Now, we are going to calculate two cases for decision parameter pk

 Case 1:  If

                         pk < 0

              Then

                          pk+1 =pk +2?y

                          xk+1 = xk +1

                          yk+1 = yk                           

Case 2:  If

                         pk >= 0

              Then

                          pk+1 =pk +2?y-2?x

                          xk+1 =xk +1

                          yk+1 =yk +1                          

Step 6: We will repeat step 5 until we found the ending point of the line and the total number of iterations =?x-1.

Step 7: Stop.

Example: A line has a starting point (9,18) and ending point (14,22). Apply the Bresenham’s Line Drawing algorithm to plot a line.

Solution: We have two coordinates,

Starting Point = (x1, y1) = (9,18)

Ending Point = (x2, y2) = (14,22)

Step 1: First, we calculate ?x, ?y.

           ?x = x2 – x1 = 14-9 = 5

             ?y = y2 – y1 = 22-18 = 4

Step 2: Now, we are going to calculate the decision parameter (pk)

   pk = 2?y-?x

                  = 2 x 4 – 5 = 3

             The value of pk = 3

Step 3: Now, we will check both the cases.

               If

                   pk >= 0

Then

         Case 2 is satisfied. Thus

                    pk+1 = pk +2?y-2?x =3+ (2 x 4) - (2 x 5) = 1

                     xk+1 =xk +1 = 9 + 1 = 10

           yk+1 =yk +1 = 18 +1 = 19

Step 4: Now move to next step. We will calculate the coordinates until we reach the end point of the line. 

?x -1 = 5 – 1 = 4

          pk          pk+1          xk+1           yk+1
9 18
3 1 10 19
1 -1 11 20
-1 7 12 20
7 5 13 21
5 3 14 22

Step 5: Stop.

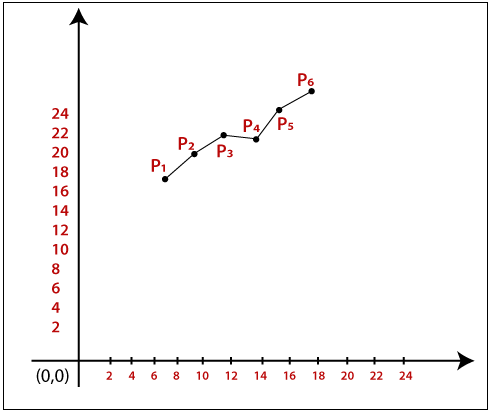
Bresenham’s Line Drawing Algorithm

The Coordinates of drawn lines are-

P1 = (9, 18)

P2 = (10, 19)

P3 = (11, 20)

P4 = (12, 20)

P5 = (13, 21)

P6 = (14, 22)

Advantages of Bresenham’s Line Drawing Algorithm

  • It is simple to implement because it only contains integers.
  • It is quick and incremental
  • It is fast to apply but not faster than the Digital Differential Analyzer (DDA) algorithm.
  • The pointing accuracy is higher than the DDA algorithm.

Disadvantages of Bresenham’s Line Drawing Algorithm

  • The Bresenham’s Line drawing algorithm only helps to draw the basic line.
  • The resulted draw line is not smooth.

Related Topics

Scan Conversion of a Circle Computer Graphics

A circle is an eight-way symmetric shape. All quadrants of a circle are the same. There are two octants in each quadrant of a circle. If we know the value of any...

3 minutes read.

Illumination Model in Computer Graphics

Illumination Model in Computer Graphics The series of methods used to depict light in computer graphics scenarios is computer graphics illumination. Although lighting strategies provide versatility in the degree of detail...

8 minutes read.

Transformation

Introduction The term Transformation is generally referred to as converting a graphic into another graphic by applying some rules or algorithms. Sometimes an image or picture can be a combination of lines, rectangle,...

2 minutes read.

Line Drawing Algorithm in Computer Graphics

“The Line drawing algorithm is a graphical algorithm which is used to represent the line segment on discrete graphical media, i.e., printer and pixel-based media.” A line contains two points....

3 minutes read.

Mid-Point Line Drawing Algorithm in Computer Graphics

The Mid-point Subdivision algorithm is the extension of the Cyrus-Beck algorithm. The Mid-Point line plotting algorithm was introduced by “Pitway and Van Aken.” It is an incremental line drawing algorithm....

8 minutes read.

DDA line Drawing Algorithm in Computer Graphics

DDA (Digital Differential Analyzer) Line Drawing Algorithm The Digital Differential Analyzer helps us to interpolate the variables on an interval from one point to another point. We can use the digital Differential Analyzer algorithm...

5 minutes read.

3D Shearing

We can denote shearing with ‘SHx,’ ‘SHy,’ and ‘SHz.’ These ‘SHx,’ ‘SHy,’ ‘SHz’ are called “Shearing factor.” The basic difference between 2D and 3D Shearing is that the 3D plane also...

1 minute read.

Types of Computer Graphics

Types of Computer Graphics The computer graphics contains two types. They are- Raster (Bitmap) graphicsVector graphics Many individuals are likely to consider pictures on computers (or phones, tablets, or some other electronic gadget...

5 minutes read.

3D Rotation

The 3D rotation is different from 2D rotation. In 3D Rotation we also have to define the angle of Rotation with the axis of Rotation. For Example- Let us assume, The initial...

2 minutes read.

2D Scaling

In scaling, we can expend or compress the size of any object. We can apply scaling on the object by multiplying the original coordinates with scaling factors. The term scaling factor...

2 minutes read.

3D Translation

A 3D Translation process contains the x-axis, y-axis, and z-axis. We can move any object from one place to another without changing the shape of the object. For Example-Translation of a...

1 minute read.

Input Devices in Computer Graphics

An Input device is the piece of computer hardware equipment used to give input to the computer. The input can be in the form of graphics, text, sound, audio, video,...

7 minutes read.

Projection in Computer Graphics

Projection Introduction: The technique projection was invented by the Swiss mathematician, engineer, and astronomer "Leonhard Euler Around" in 1756. The "Episcope" was the first projection system. “Projection is a technique or process which...

4 minutes read.

Polygon Clipping in Computer Graphics

“A Polygon can be described as the enclosed collection or group of the lines.” In a polygon, all lines are connected. Lines can be a combination of edges and vertices,...

4 minutes read.

Scan Conversion in Computer Graphics

“When we represent regular objects in the form of discrete pixels, it is called Scan Conversion.” Every graphics system must transform the primitives into a collection of pixels. The scan conversion is also...

2 minutes read.

Image Representation in Computer Graphics

Image Representation: In computer science, we can represent an image in various forms. Most of the time, it refers to the way that brings information, such as color is coded digitally, and...

4 minutes read.

Display Processor

It is a part of hardware or interpreter which is used to transform display processor code into pictures. It is used to convert digital information from CPU to analog data. It...

4 minutes read.

2D Translation

We can move any object from one to another place without changing the shape of the object. For Example- Translation of a Point:If we want to translate a point from P (x0,...

1 minute read.

Bresenham’s Circle Drawing Algorithm in Computer Graphics

Bresenham’s algorithm is also used for circle drawing. It is known as Bresenham’s circle drawing algorithm. It helps us to draw a circle. The circle generation is more complicated than...

11 minutes read.

3d Scaling

The 2D and 3D scaling are similar, but the key difference is that the 3D plane also includes the z-axis along with the x and y-axis. In scaling, we can expend...

2 minutes read.