Composite Transformation in Computer Graphics

Composite transformation in Computer Graphics

It is possible to integrate a range of transformations or series of transformations into some kind of a single one which is known as composition. The combined matrix is known as the resultant matrix. The merger procedure is termed as concatenation.

Assume that we want to execute rotation around an arbitrary point, and we'll do it through a series of following three transformations.

• Translation
• Rotation
• Reverse Translation

The arranging pattern of these transformation numbers should not be modified. If a matrix is expressed in a column’s format, the composite transformation is carried out, by multiplying the sequence of the matrix from the right-hand side to the left-hand side. The output of the former matrix is multiplied by the new matrix that will come.

Instances of Composite Transformation

The enhancement has to do with the center. The following series of transformations will also be carried out and all will be integrated into a single one.

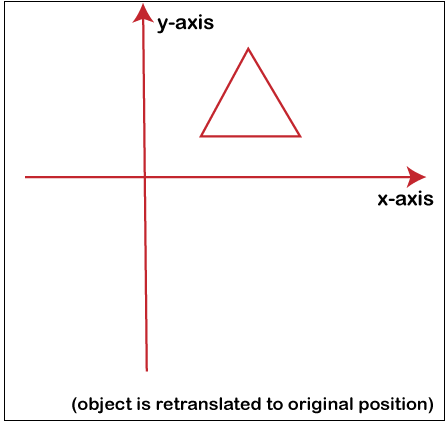
Phase 1: As shown in the image (1), the entity is preserved in its location

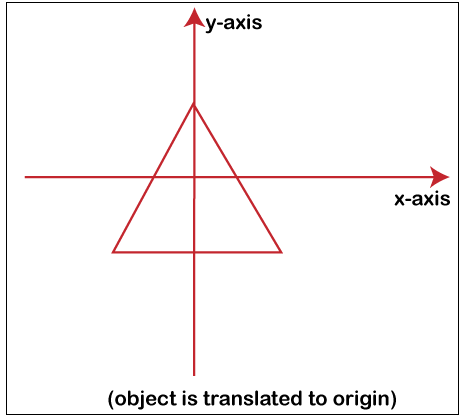
Phase 2: The entity is transformed so that, as displayed in the image (2), its center correlates with the origin.

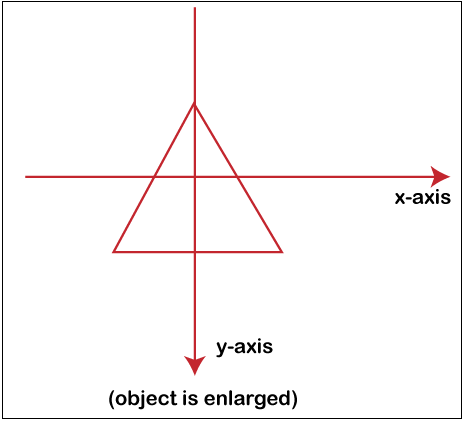
Phase 3: The scaling of an entity is accomplished in Image (3) by holding the entity at its source.

Phase 4: The translation is completed once again. The next translation is known as a reverse translation. It will place the entity at the location of its center point.

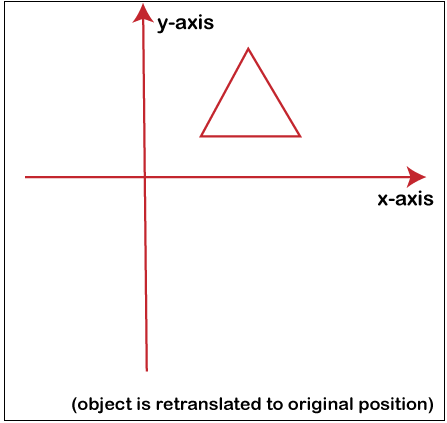
The above­-given transformation can be defined as T_v.ST_v^-1.

Important Point:

For expressing matrices, two kinds of rotations are used: one will be the column form. The Row Method will be another form.

Here we will discuss both formats one by one.

• Column Format

The matrix of the column method is-

1. Translation

           1    0     T_x

           0    1     T_y                     

           0    0     1

• Scaling

           1    0     S_x

           0    1     S_y                     

           0    0     1

• Row Format

The matrix of the row method is-

1. Translation

           1     0      0

           0     1      0                     

           T_x   T_x    1

• Scaling

           1      0      0

           0      1      0                     

           S_x     S_y    1

Benefits of Combined or Concatenated matrix

• The adjustments are lightweight.
• It will decrease operations.
• In contrast to the matrix, the principles used for describing transformation in the form of equations are complicated.

Assembling of two translations

Let the translation equations be T1 T2 T3 T4. These are the two Q1 and Q2 translations. The following matrix of Q1 and Q2 is given. Using homogeneous matrices, Q1 and Q2 are described, and Q will be the last transformation matrix received after multiplication.

            1     0      T₁                                                                 1     0      T₃  

Q₁ =     0     1      T₂                            Q₂ =         0     1      T₄                    

            0     0      1                                               0     0      1   

                                                 1      0      T₁ + T₂

   Q =      0      1      T₃ + T₄                     

                                                 0      0          1

The resulting matrix mentioned above demonstrates that two consecutive translations are complementary.

Two Rotation concentration: Two Rotations are both additives.  

Composition of two scaling

There is a multiplicative combination of 2 scaling. Let the whole matrix be multiplied by R11 and R12.

             R₁      0      0                          S₃      0      0 

 R₁₁ =    0       R₂     0            R₁₂ =     0       S₄     1

              0       1      0                           0       0      1

R = R_{11 ­}* R₁₂ = R₁₁ (R₁.R₂). R₁₂ (R₃. R₄) = R (R₁. R₂. R₃. R₄)