Midpoint Circle Drawing Algorithm in Computer Graphics

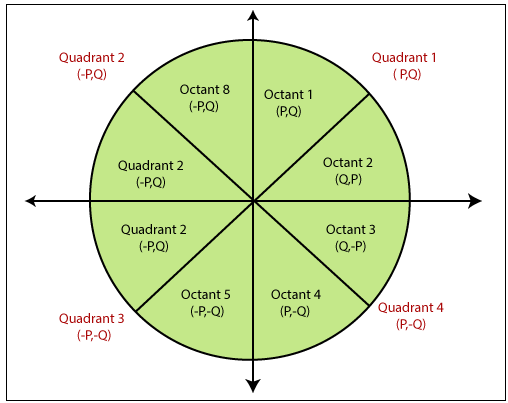
The midpoint circle drawing algorithm helps us to calculate the complete perimeter points of a circle for the first octant. We can quickly find and calculate the points of other octants with the help of the first octant points. The remaining points are the mirror reflection of the first octant points.

This algorithm is used in computer graphics to define the coordinates needed for rasterizing the circle. The midpoint circle drawing algorithm helps us to perform the generalization of conic sections. Bresenham’s circle drawing algorithm is also extracted from the midpoint circle drawing algorithm. In the algorithm, we will use the 8-way symmetry property.

In this algorithm, we define the unit interval and consider the nearest point of the circle boundary in each step.

Let us assume we have a point a (p, q) on the boundary of the circle and with r radius satisfying the equation f_c (p, q) = 0

As we know the equation of the circle is –

f_c (p, q) = p² + q² = r²     …………………………… (1)

If

     f_c (p, q) < 0

then

      The point is inside the circle boundary.

If

     f_c (p, q) = 0

then

      The point is on the circle boundary.

If

     f_c (p, q) > 0

then

      The point is outside the circle boundary.

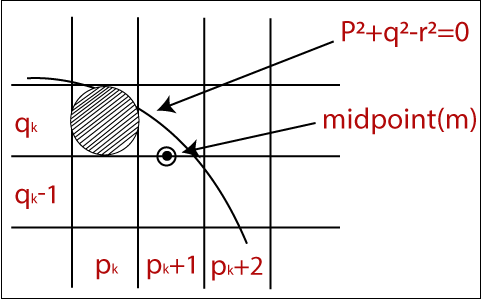
In the figure, we calculate the mid-point (m). The midpoint appears between q_k and q_k -1.

The currentposition of the pixel = p_k +1

The next position of the pixel = (p_k +1, q_k) and (p_k +1, q_k - 1)

Now, we will calculate the decision parameter (d_k)

d_k = (p_k +1, q_k – 1/2)

Now, we replace all the values with equation (1)

d_k = (p_k +1)² + (q_k – 1/2)² – r^{2                          ……………………………………} (2)

Now, there should be two conditions.

Condition 1: If

                          d_k is negative

                     then

                            The midpoint (m) is inside the circle boundary    

Condition 2: If

                          d_k is positive

                     then

                            The midpoint (m) is outside the circle boundary    

Now, we find the next point of x coordinates. Then,

P_k+1 +1 = P_k+2

Now, we replace all the value of equation (2) with (k+1). We get-

 d_k+1 = (p_k+1 +1)² + (q_k+1 – 1/2)² – r²                ……………………………. (3)

Now, we will find the difference between

d_k+1 – d_k = {(p_k+1 +1)² + (q_k+1 – 1/2)² – r²} – {(p_k +1)² + (q_k – 1/2)² – r²}

               = d_k +(2p_k +1) + (q_k+1² – q_k²) – (q_k+1 – q_k) +1    …………………… (4)

Here, If

                    d_k isnegativethen d_k+1

          then

                    2p_k+1 +1

Otherwise      

                    2p_k+1 +1 – 2q_k+1

Now, the next coordinate for x and y points

2p_k+1 = 2p_k +2

2q_k+1 = 2q_k –2

Now, the initial decision parameter (d₀) at the position (p, q) = (0, r)

We put (0, r) in circle equation and we get-

d₀ = (1, r – 1/2)

    = (1 + (r –1/2)² –r²)

    = 5/4 –r  

We only take integer value = 1 – r

Algorithm of Midpoint Circle Drawing

Step 1: Start.

Step 2: First, we allot the center coordinates (p₀, q­₀) as follows-

             P₀ = 0

             q₀ =r

Step 3: Now, we calculate the initial decision parameter d₀ -

                                                                 d₀ = 1 – r

Step 4: Assume,the starting coordinates = (p_k, q_k)

                  The next coordinates will be (p_k+1, q_k+1) 

Now, we find the next point of the first octant according to the value of the decision parameter (d_k).      

Step 5: Now, we follow two cases-

Case 1: If

                  d_k < 0

         then

                  p_k+1 =p_k + 1

                  q_k+1 =q_k

                  d_k+1 = d_k + 2 p_k+1 + 1

Case 2: If

                  d_k >= 0

         then

                  p_k+1 =p_k + 1

                  q_k+1 =q_k –1

                  d_k+1 = d_k - 2 (q_k+1 + 2 p_k+1)+ 1

Step 6: If the center coordinate point (p₀, q₀) is not at the origin (0, 0) then we will draw the points as follow-

For x coordinate = x_c + p₀

For y coordinate = y_c + q₀                    {x_c andy_c containsthe current value of x and y coordinate}

Step 7: We repeat step 5 and 6 until we get x>=y.

Step 8: Stop.

Example: The center coordinates are (0, 0), and the radius of the circle is 10. Find all points of the circle by using the midpoint circle drawing algorithm?

Solution:

Step 1: The given center coordinates of the circle (p_0, q₀) = (0, 0)

              Radius of the circle (r) = 10

Step 2: Now, we will determine the starting coordinates (p_0, q₀) as follows-

             P₀ = 0

             q₀ = r (radius) = 10

Step 3: Now, we will determine the initial decision parameter (d₀)

                                d₀ = 1 –r

                    d₀ = 1 –10

                    d₀ = -9

Step 4: The initial parameter d₀ < 0 then, case 1 is satisfied.

           p_k+1 =p_k + 1 = 0 + 1 = 1

                  q_k+1 =q_k = 10

                  d_k+1 = d_k + 2 p_k+1 + 1 = -9 + 2(1) + 1 = -6

Step 5: The center coordinates of circle are already (0, 0). So, move to next step.

Step 6: We will execute step 4 until we get x >= y.

The table for coordinates of octant 1-

dk	dk+1	(pk+1,qk+1)
		(0, 10)
­-9	-6	(1, 10)
-6	-1	(2, 10)
-1	6	(3, 10)
6	-3	(4, 9)
-3	8	(5, 9)
8	5	(6, 8)

Now, we will determine the coordinates of the octant 2 by swapping the p and q coordinates.

Points of Octant 1	Points of Octant 2
(0, 10)	(8, 6)
(1, 10)	(9, 5)
(2, 10)	(9, 4)
(3, 10)	(10, 3)
(4, 9)	(10, 2)
(5, 9)	(10, 1)
(6, 8)	(10, 0)

Thus, we can find all the coordinates of the circle for all quadrants.

Quadrant 1 (p, q)	Quadrant 2 (-p, q)	Quadrant 3 (-p, -q)	Quadrant 4 (p, -q)
(0, 10)	(0, 10)	(0, -10)	(0, -10)
(1, 10)	(-1, 10)	(-1, -10)	(1, -10)
(2, 10)	(-2, 10)	(-2, -10)	(2, -10)
(3, 10)	(-3, 10)	(-3, -10)	(3, -10)
(4, 9)	(-4, 9)	(-4, -9)	(4, -9)
(5, 9)	(-5, 9)	(-5, -9)	(5, -9)
(6, 8)	(-6, 8)	(-6, -8)	(6, -8)
(8, 6)	(-8, 6)	(-8, -6)	(8, -6)
(9, 5)	(-9, 5)	(-9, -5)	(9, -5)
(9, 4)	(-9, 4)	(-9, -4)	(9, -4)
(10, 3)	(-10, 3)	(-10, -3)	(10, -3)
(10, 2)	(-10, 2)	(-10, -2)	(10, -2)
(10, 1)	(-10, 1)	(-10, -1)	(10, -1)
(10, 0)	(-10, 0)	(-10, 0)	(10, 0)

Advantages of Midpoint circle drawing algorithm

• It is a powerful and efficient algorithm.
• The midpoint circle drawing algorithm is easy to implement.
• It is also an algorithm based on a simple circle equation (x² + y² = r²).
• This algorithm helps to create curves on a raster display.

 Disadvantages of Midpoint circle drawing algorithm

• It is a time-consuming algorithm.
• Sometimes the points of the circle are not accurate.

Related Post:

• Scan Conversion of an Ellipse Computer Graphics
• Scan Conversion of a Circle Computer Graphics
• Bresenham’s Circle Drawing Algorithm in Computer Graphics
• Line Drawing Algorithm in Computer Graphics
• DDA line Drawing Algorithm in Computer Graphics
• 3D Rotation in Computer Graphics
• 2D Rotation in Computer Graphics
• Computer Graphics Tutorial
• Projection in Computer Graphics
• Animation in Computer Graphics