Scan Conversion of a Circle Computer Graphics

A circle is an eight-way symmetric shape. All quadrants of a circle are the same. There are two octants in each quadrant of a circle. If we know the value of any point, then we can easily calculate the values of the remaining seven points by using the eight-way symmetry method. A circle is a shape consist of a line called the circumference. All the straight lines drawn from a particular point within the circle to the circumference are always equal. A circle is a round shape that has no corner or sides.

“A circle can be defined as a combination of points that all points are at the same distance (radius) from the center point.” We can express a circle by the following equation-

                                (P - P_c)² + (Q - Q_c)² = r²_­­­

The above equation can be written as-

                                (P)² + (Q)² = r²_{­ ­}                                                  {r = radius}

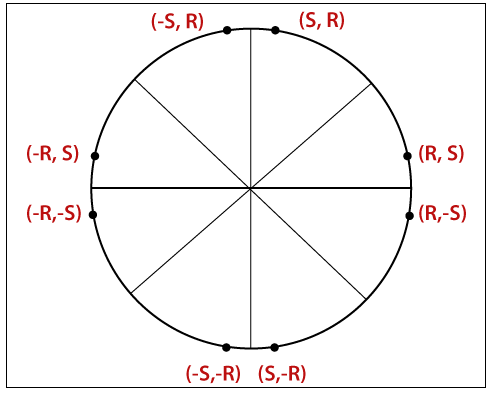
If we want to draw a circle, then we will consider it by its origin point. Let us assume a point P₁(R, S) then we can represent the other seven points as follows-

P₂(R, -S)

P₃(-R, -S)

P₄(-R, S)

P₅(S, R)

P₆(S, -R)

P₇(-S, -R)

P₈(-S, R)

We can also represent eight points of the circle on the computer screen by using of put pixel function ().

Putpixel (R, S, Color)                                    

Putpixel (R, -S, Color)

Putpixel (-R, -S, Color)

Putpixel (-R, S, Color)

Putpixel (R, S, Color)

Putpixel (R, -S, Color)

Putpixel (-R, -S, Color)

Putpixel (-R, S, Color)

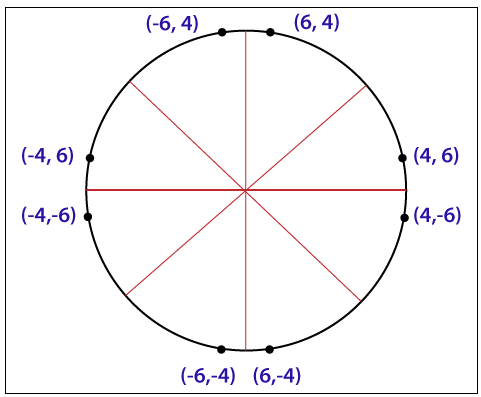
Example: Let, we have taken a point (4, 6) of a circle. We will calculate the remaining seven points by using of reflection method as follows-

The seven points are – (4, -6), (-4, -6), (-4, 6), (4, 6), (4, -6), (-4, -6), (-4, 6)

There are two following standard methods to define a circle mathematically.

• A circle with a second-order polynomial equation.
• A circle with trigonometric/ polar coordinates.

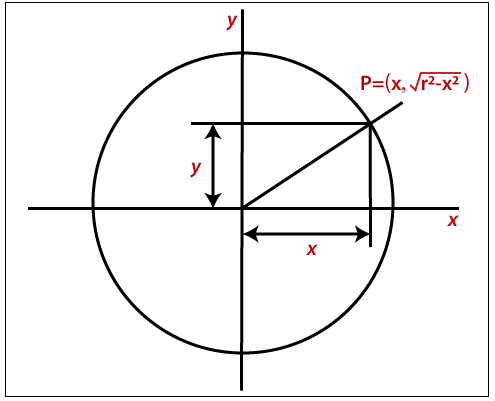
A circle with the second-order polynomial equation-

                                  y² =r² – x²

Here, x = The coordinates of x

         y = The coordinates of y

r = The radius of the circle

In this method, we will find the x coordinate (90° to 45°) by moving x from 0 to r/?2, and we will find each y coordinate by calculating ?r²-x² for each step.

It is an ineffective method because for each point x coordinate and radius r must be squaredand subtracted from each other. 

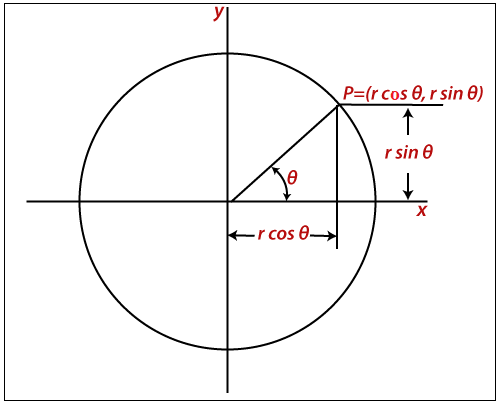
A circle with trigonometric/polar coordinate-

x = r cos ? 

y = r sin ?

Here, x = The coordinate of x

        y = The coordinate of y

          r = The radius of the circle

          ? = Current angle

In this method, the value of ? moves from 0 to ?/4. We will calculate each value of x and y.

Algorithms used in Circle Drawing

There are the following two algorithms used to draw a circle.

• Bresenham’s Circle drawing Algorithm  
• Mid-point Circle Drawing Algorithm