Base Conversion in Number System
Base Conversion in Number System: In previous topic, we have learnt about different number systems. In this topic, we will learn how to convert one number system into another, such as Binary number to Decimal, and this process is called Base conversion.
Need for Base Conversion
In the real world, let suppose there are two persons, one is proficient in the German language, and the other is proficient in the English language. If both the persons wish to communicate with each other, they require a translator to convert English to German and vice-versa. Similarly, in digital systems, most of the circuits use a binary number system. But some people understand the digital number system easily. So, there is a need for a translator to convert the data from one number system to another. Encoders and decoders are widely used for the conversion.
For example, calculators contain encoders and decoders to convert the data electronically from decimal to binary and vice-versa.
Block diagram using encoder and decoder

Let’s see different base conversions with example:
Binary to Decimal conversion
The conversion of binary to decimal can be performed simply by summing together, the integral and fractional parts are multiplied by ‘2i’ where the value of ‘i’ depends on the position.
| Convert (1100.1011)2 into the decimal number system. (1100.1011)2 = (1 x 23 + 1 x 22 + 0 x 21 + 0 x 20 + 1 x 2-1 + 0 x 2-2 + 1 x 2-3 + 1 x 2-4)10 |
| = (8 + 4 + 0 + 0 + 0.5 + 0 + 0.125 + 0.0625)10 |
| = ( 12.6875 )10 |
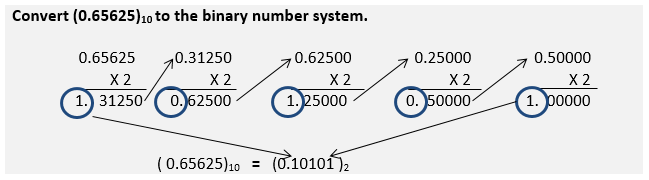
Decimal to Binary conversion
Divide the integral parts repeatedly by ‘2’ and write down the remainders after every division until ‘0’ is obtained as a quotient.
For the fractional part, multiply by the fraction part by ‘2’ until we obtain ‘1’ as a result.

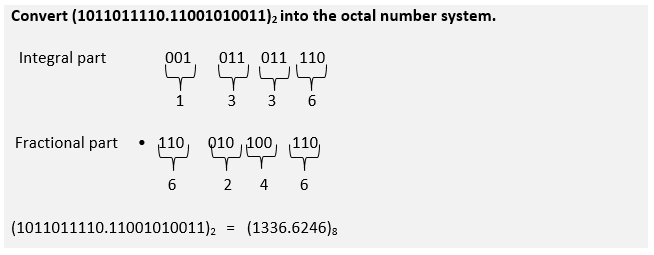
Binary to Octal conversion
Binary bits are grouped into groups of three, initiated from LSB for an integral part, and the fractional part grouping initiates from MSB.
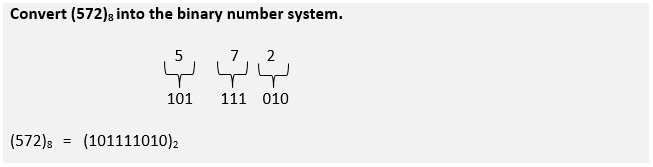
Octal to Binary conversion
Octal bits are split into groups of three initiated from LSB for an integral part, and the fractional part grouping initiates from MSB.
Octal to Decimal conversion
| Convert (6327.4051)8 to the decimal number system. (6327.4051)8 = (6 x 83 + 3 x 82 + 2 x 81 + 1 x 80 + 4 x 8-1 + 0 x 8-2 + 5 x 8-3 + 1 x 8-4)10 |
| = (3072 + 192 + 16 + 7 + 0.5 + 0 + 0.00976 + 0.00024)10 |
| = ( 3287.5100098 )10 |
Decimal to Octal conversion
Divide the integral parts repeatedly by ‘8’ and write down the remainders after every division until ‘0’ is obtained as a quotient.
For the fractional part, multiply by the fraction part by ‘8’ until we obtain ‘1’ as a result.

Hexadecimal to Decimal conversion
| Hexadecimal | Decimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
| Convert (3A.2F)16 to the decimal number system. (3A.2F)16 = (3 x 161 + 10 x 160 + 2 x 16-1 + 15 x 16-2)10 |
| = ( 48 + 10 + 0.125 + 0.05859)10 |
| = ( 58.1836 )10 |
Decimal to Hexadecimal conversion
Divide the integral parts repeatedly by ‘16’, and write down the remainders after every division until ‘0’ is obtained as a quotient.
For the fractional part, multiply by the fraction part by ‘16’ until you obtain ‘1’ as a result.

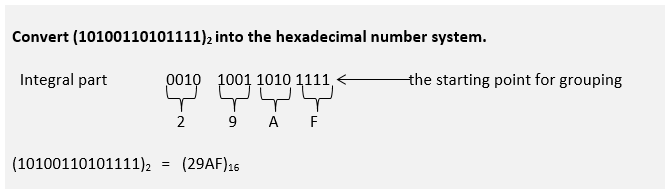
Binary to Hexadecimal conversion
Binary bits are grouped into groups of four initiated from LSB for an integral part, and the fractional part grouping initiates from MSB.
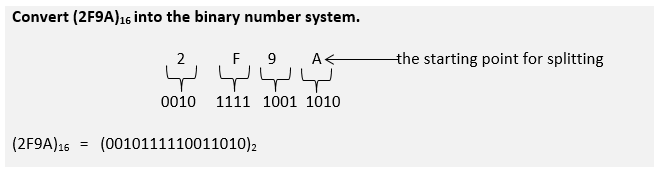
Hexadecimal to Binary conversion
Hexadecimal bits are split into groups of four initiated from LSB for an integral part, and the fractional part grouping initiates from MSB.
| Takeaway Points: - The integer part will increase whenever there is a conversion from a higher base to a lower base and vice-versa. The fraction part will decrease whenever there is a conversion from a higher base to a lower base and vice-versa. |