Data Representation in Digital Electronics
Data Representation in Digital Electronics
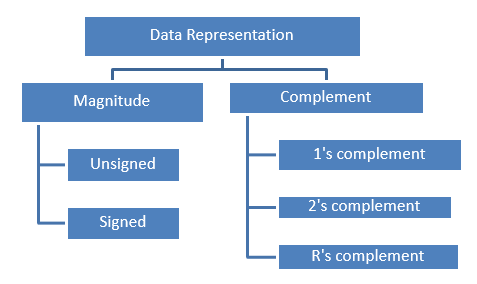
In digital electronics, we can represent the data in following ways:
In the conventional arithmetic system, a negative number is represented by a minus sign and a positive number by a plus sign. But in digital systems, computers take input data in the form of binary, also referred to as ‘bits.’
Unsigned Magnitude
It is only used for positive numbers. For n-bits, the range varies from 0 to 2n – 1.
e.g., “9” is represented as 01001.
Signed Magnitude
In this type, positive numbers are represented with normal binary and their MSB as ‘0’ and negative numbers with MSB as ‘1’. For n-bits, its range varies from - (2n-1 – 1) to + (2n-1 – 1).
e.g., “+9” is represented as 01001.
e.g., “-9” is represented as 11001.
Note: -‘11001’ is equivalent to ‘25’ only when considered an unsigned number.
Complement
In digital systems, complements are very useful in simplifying the subtraction operation and other logical manipulations. In digital electronics, there are different ways of complements are possible, and these ways are:
- 1’s Complement
- 2’s Complement
- R’s Complement
1’s Complement
In the binary, if we replace each ‘0’ by ‘1’ and it’s vice-versa, the final result is the 1’s complement of the original binary number.
In this type, positive numbers are represented with normal binary and their MSB as ‘0’ and negative numbers with MSB as ‘1.’ To find the 1’s complement of a negative number, we have to follow a few steps:-
Step 1:- Write binary of positive number.
Step 2:- Its 1’s complement
| Find 1’s complement of -13. Step 1:- +13 = 01101 Step 2:- -13 = 10010 (1’s complement) |
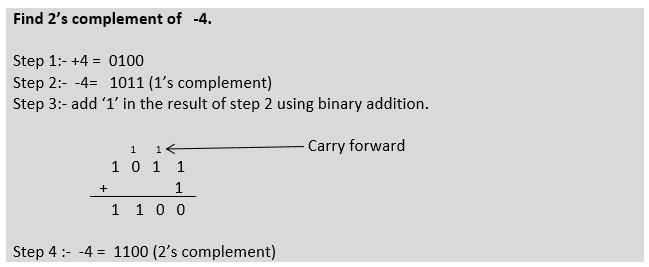
2’s Complement
By adding ‘1’ to the one’s complement representation of a binary number, we will obtain the final result as 2’s complement of the original number.
In this type, positive numbers are represented with normal binary and their MSB as ‘0’ and negative numbers with MSB as ‘1.’ To find the 2’s complement, but to represent a negative number, we have to follow a few steps:-
Step 1:- Write binary of positive number.
Step 2:- It’s 1’s complement.
Step 3:- add ‘1’ in the result of step 2 using binary addition.
R’s complement
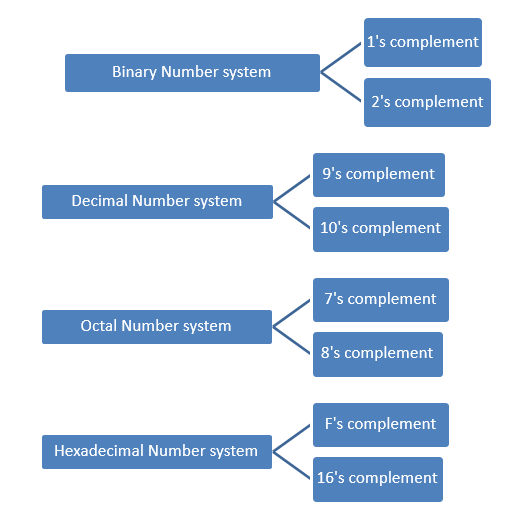
Here ‘R’ is depicting radix or base. The R’s complement is further sub-classified into two types:-
- (R-1)’s complement
- R’s complement
1. (R-1)’s complement
We need to follow a few steps to find the (R-1)’s complement of any number.
Step 1: - For the given base number system, write the maximum possible number.
Step 2:- Subtract the given number from the maximum possible number.
Example 1
Find the 9’s complement of a decimal number 2669.
Solution:-
Step 1:- In a decimal number system maximum possible 4 digit number is 9999.
Step 2:- Subtract 2669 from 9999.
We obtain 9’s complement as = 9999 - 2669
= 7330
Example 2
Find the 7’s complement of an octal number 5667.
Solution:-
Step 1:- In an octal number system maximum possible 4 digit number is 7777.
Step 2:- Subtract 5667 from 7777.
We obtain 7’s complement as = 7777 - 5667
= 2110
Example 3
Find the F’s complement of Hexadecimal number 2688.
Solution:-
Step 1:- In a hexadecimal number system maximum possible 4 digit number is FFFF.
Step 2:- Subtract 2688 from FFFF.
We obtain F’s complement as = FFFF - 2668
= D977
2. R’s complement
We need to follow a few steps to find the R’s complement of any number. These steps are very similar to 2’s complement.
Step 1: - For the given base number system, write the maximum possible number.
Step 2:- Subtract the given number from the maximum possible number.
Step 3:- add ‘1’ in the result of step 2 using binary addition method.
Example 4
Find the 8’s complement of an octal number 2669.
Solution:-
Step 1:- In a decimal number system maximum possible 4 digit number is 7777.
Step 2:- Subtract 2669 from 7777.
We obtain 7’s complement as = 7777 - 2669
= 5108
Step 3:- adding ‘1’ in 5108, to obtain the 8’s complement.
8’s complement = 5108 + 1
= 5109 (but it is not in octal form)
8‘s complement in octal form = 5111.