Codes in Digital Electronics

CODES

In digital system, the data or information such as numbers, letters, characters, or punctuation marks are depicted by a unique or particular set of symbols. They are fundamentally encrypted and, therefore, the group of symbols is considered as "CODE." In he digital system, encrypted means ‘encoded.’ This encoding or decoding is achieved using the encoder or decoder in the digital circuits.

• Non-Binary

E.g., Morse code: - a series of dots and dashes are used to represent data.

• Binary

E.g., Gray Code, BCD, Excess-3 Code, 8-4-2-1 code, Error detecting and correcting codes

• Alphanumeric

E.g., Boudet’s (5-bit Code), ASCII Code (7 bit+ 1-bit parity), EBCDIC (8 bit)

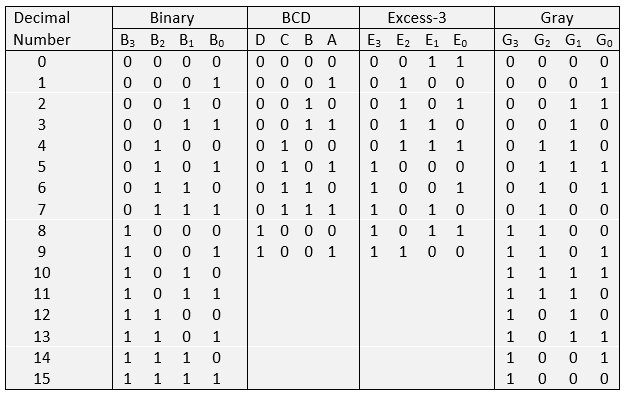
Binary Coded Decimal Code (BCD)

In BCD, each digit of a decimal number is represented by a binary equivalent. It's a 4-bit code, which is additionally called 8-4-2-1 code. The best thing is that it is relatively simple converting to and from decimal. It falls within the weighted code system category. They're utilized in calculators, counters, digital voltmeters, digital clocks, etc.

Decimal to BCD conversion

Excess-3 Code

It is a 4-bit code. This can be derived easily from the BCD code by adding “3” to every digit of the coded number. It is a self-complementing code, which implies that the one’s complement of an excess-3 number is similar to the excess-3 code for the 9’s complement of the corresponding decimal number. It falls in the unweighted code system category.

Decimal to Excess-3 conversion

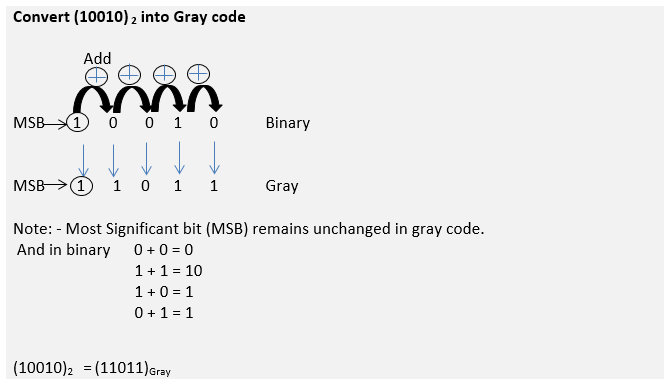
Gray Code

It is a very useful code in which the code group changes only 1 bit when moving from one point to another point-also known as “Reflected Code” or “Minimum change code.” It is generally used in Input/output devices, instrumentations such as shaft encoders to calculate angular displacement, and in linear encoders to calculate linear displacement. It falls in the unweighted code system category.

Binary to Gray Code conversion

Starting from leftward and moving towards rightward, add each adjacent pair of binary digits to get gray code digit.

Alphanumeric Codes

Sometimes data is represented in the mixed form of numbers, alphabets, and special characters. It is also known as “Internal code”, because representing data in the form of alphanumeric characters and symbols is an internal process. Most commonly used such codes are:-

1. Extended BCD Interchange Code (EBCDIC):- It is 8-bit code. It can represent 2⁸=256 possible Characters.

• American Standard Code for Information Interchange:- It is most widely used in many mainframes having a 7-bit code. It can represent 2⁷=128 possible Characters. They are also pronounced as ASCII (ask-ee).

Error Detecting Code

When data flows from Transmitter points to Receiver point, errors are occurred due to the electrical noise in the system. The simplest and widely used scheme for detecting this type of error is the “Parity method.” An extra bit or called a “Parity bit,” is combined with the original transmitted code to make the total count of “1’s” to be even or odd.

Note: - This method has some limitations. It will not work if two bits are in error.

Error Correcting Code

This type of code does both tasks, such as finding the error as well as correcting it. The “HAMMING CODE” is the most widely used. This code is generated for a group of n-bit data by adding ‘k’ parity or check bits to make a form of (n+k)-bit code.  The magnitude of ‘k’ is selected in such a way that it can describe (n+k) possible error bit locations and also helps to determine the “no error” condition. Inequality for choosing the value of ‘k’ is:-

                                             2^k ? n+k+1