ElGamal Algorithm

What is ElGamal Algorithm?

ElGamal Algorithm is an asymmetric key encryption technique for communicating between two parties and encrypting the message. With the help of cryptography, the employee can communicate securely. In encryption, the plain text is converted to encrypted text. The encrypted text is converted back to plain text with the help of a decryption algorithm. The encryption and decryption key need to be secure. There are two types of cryptography. These two are as follows:

• Symmetric cryptography: There is one shared key used for both encryption and decryption.
• Asymmetric cryptography: There are two keys (private key and public key) where one of the keys is for encryption and the other for decryption.

For asymmetric cryptosystems, we require public-key encryption to start the communication. One of these public-key encryption schemes is the ElGamal encryption based on the Diffie-Hellman Key exchange protocol for symmetric cryptosystems.

ElGamal encryption is a public key cryptosystem. It uses the method of asymmetric key encryption to encrypt the message. This cryptosystem is based on the finding of discrete logarithm. If we have two groups, g^a and g^k, it is much more challenging to find the value of g^ak. 

The idea of the ElGamal Cryptosystem

Let's take an example to understand this. There are two siblings, Alex and Lucy. Suppose Alex want to communicate with Lucy.

1. First, Lucy has to generate one public and one private key.

• Lucy has to choose a large number, "q", and a cyclic group F_q.
• Then she has to choose any element "g" from the cyclic group. 
• She has to choose another element, "a", such that gcd(a,q)=1.
• Then she has to compute the value of "h", h=g^a.
• Then Lucy publishes the value of F, h=g^a, q and g in her public key and "a" as a private key.

2. Then Alex has to encrypt the data using Lucy's public key.

• Alex has to select the element "K" from the cyclic group "F" in such a way that gcd(k,q)=1.
• Then Alex has to compute p = g^k and s = h^k = g^ak. Then he has to multiply the value of s and M.
• Then he has to send (p, M*s) = (g^k, M*s).

3. Lucy has to decrypt the message.

• Lucy has to calculate s' = p^a = g^ak.
• Lucy has to divide M*s by s' to obtain M as s = s'.

Implementation of ElGamal encryption In Python

Example:

import random
from math import pow
	
a = random.randint(2, 10)


def gcd(a, b):
	if a < b:
		return gcd(b, a)
	elif a % b == 0:
		return b;
	else:
		return gcd(b, a % b)




def gen_key(q):


	key = random.randint(pow(10, 20), q)
	while gcd(q, key) != 1:
		key = random.randint(pow(10, 20), q)


	return key
def power(a, b, c):
	x = 1
	y = a


	while b > 0:
		if b % 2 != 0:
			x = (x * y) % c;
		y = (y * y) % c
		b = int(b / 2)


	return x % c
def encrypt(msg, q, h, g):


	en_msg = []


	k = gen_key(q)
	s = power(h, k, q)
	p = power(g, k, q)
	
	for i in range(0, len(msg)):
		en_msg.append(msg[i])


	print("g^k used : ", p)
	print("g^ak used : ", s)
	for i in range(0, len(en_msg)):
		en_msg[i] = s * ord(en_msg[i])


	return en_msg, p


def decrypt(en_msg, p, key, q):


	dr_msg = []
	h = power(p, key, q)
	for i in range(0, len(en_msg)):
		dr_msg.append(chr(int(en_msg[i]/h)))
		
	return dr_msg
def main():


	msg = 'encryption'
	print("Original Message :", msg)


	q = random.randint(pow(10, 20), pow(10, 50))
	g = random.randint(2, q)


	key = gen_key(q)
	h = power(g, key, q)
	print("g used : ", g)
	print("g^a used : ", h)


	en_msg, p = encrypt(msg, q, h, g)
	dr_msg = decrypt(en_msg, p, key, q)
	dmsg = ''.join(dr_msg)
	print("Decrypted Message :", dmsg);




if __name__ == '__main__':
	main()

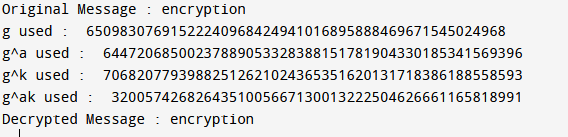
Output:

Conclusion

In this cryptosystem, the original message M is masked by multiplying g^ak to it. To remove the mask, a clue is given in form of g^k. Unless someone knows a, he will not be able to retrieve M. This is because finding discrete log in a cyclic group is difficult and simplifying knowing g^a and g^k is not good enough to compute g^ak.