Bipartite Graph

A graph is said to be bipartite if and only if we can divide all the vertices of a graph into two sets such that these sets are mutually exclusive and exhaustive, and all the edges of the graph are cross sets, and not a single edge should be in the same set.

It means let's suppose we have N vertices in a graph, and we divide them into two sets, S1 and S2 then.

 and  and every edge should be from S1 to S2.

For example: 

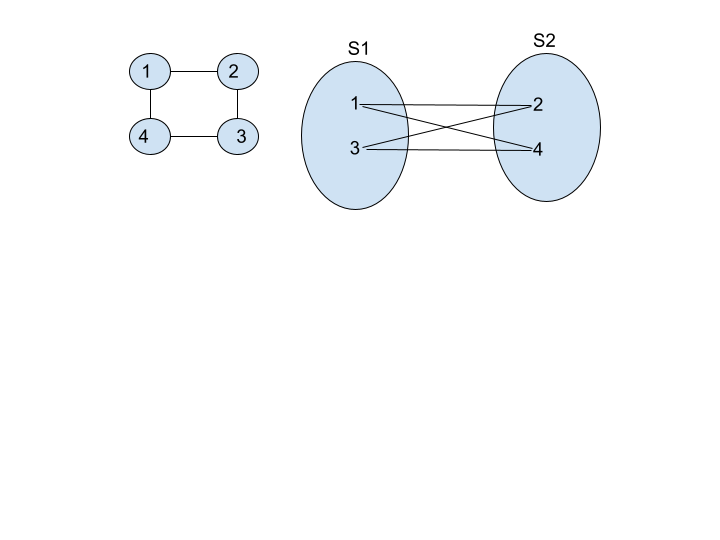
In the above graph, we can see that we divide the vertices into two sets, S1 and S2. They are mutually exclusive and exhaustive. Also, there is no edge belonging to the same set. All the edges are cross-sets. So this graph is a bipartite graph.

Another simplest definition of a bipartite graph is that if we can color the graph with only two colors and adjacent vertices should not have the same color, then it is bipartite, else it is not bipartite.

For example:

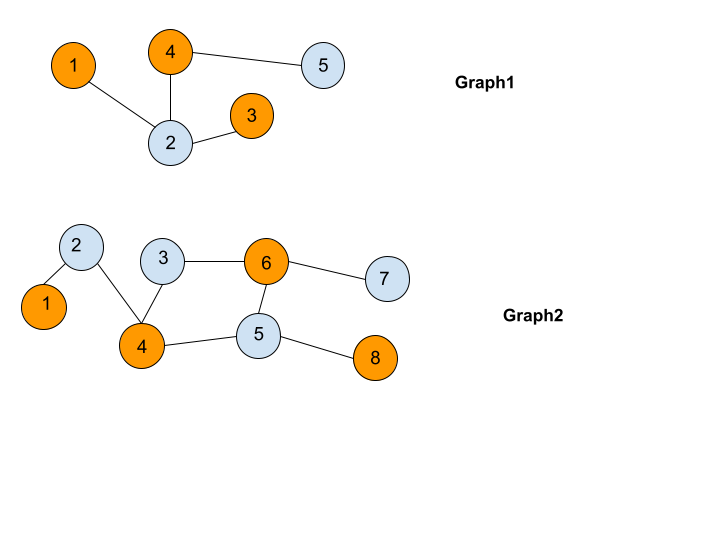
In the above examples, both graph 1 and graph 2 are both bipartite. Graph 1 and graph 2 both can color with just 2 colors and no adjacent vertices have the same color.

Graph 1 is acyclic, and Graph 2 has a cycle.

But we can see the cycle length in graph 2 is 4, which is even.

So, we can conclude that if a graph is acyclic or it has an even length cycle, then it is bipartite else, it is not bipartite.

For example:

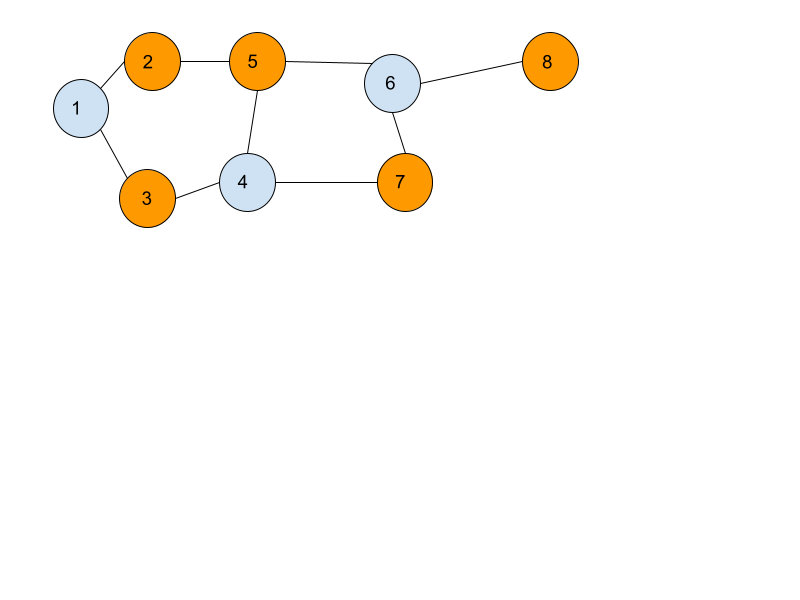
In the graph, we will see that at vertex 5, we can’t use any color because it violates our condition. The above graph is not bipartite. We can see that there are two cycles in the above graph. The first cycle has a length of 5 and the second cycle has a length of 4. So length 5 cycle has the problem so that we can say, “if a graph has an odd length cycle, it will definitely not be bipartite else, it will be bipartite.

For code implementation, we will use BFS/DFS traversal. From the source node when we are starting the traversal, then we will color it either 0 or 1. After that see for its adjacent neighbors, if its adjacent is unvisited, then make their color different and call DFS for them. If adjacent nodes have the same color, return false otherwise return true.

DFS Code in JAVA

import java.util.*;
public class Main{
    public static void main(String[] args){
         int n = 5;
        ArrayList < ArrayList < Integer >> graph = new ArrayList < ArrayList < Integer >> ();


        for (int i = 0; i < n+1; i++)
            graph.add(new ArrayList < Integer > ());


        graph.get(1).add(2);
        graph.get(2).add(1);


        graph.get(2).add(3);
        graph.get(3).add(2);


        graph.get(3).add(4);
        graph.get(4).add(3);


        graph.get(4).add(5);
        graph.get(5).add(4);
        
        graph.get(5).add(1);
        graph.get(1).add(5);


        System.out.println(isBipartite(graph,n));
    }
    
    public static boolean isBipartite(ArrayList<ArrayList<Integer>> graph,int n){
        
        int[] color=new int[n+1];
        Arrays.fill(color,-1);
        for(int i=1;i<=n;i++){
            if(color[i]==-1){
                color[i]=0;
                if(dfs(graph,color,i)==false)
                return false;
            }
        }
        return true;
    }
    public static boolean dfs(ArrayList<ArrayList<Integer>> graph,int[] color,int node){
        
        for(int nbr: graph.get(node)){
            if(color[nbr]==-1){
                color[nbr]=1-color[node];
                if(dfs(graph,color,nbr)==false) 
                  return false;
            }else if(color[nbr]==color[node]){
                return false;
            }
        }
        return true;
    }
}

Time complexity

As we are traversing all the nodes, suppose the total number of nodes is N and the edge is E.

So time complexity would be: O(N+E).

Space complexity

O(N) for color array, O(N) for recursive stack space, and O(2*E) for 2d array list of graphs.

So if we ignore the space for the graph, then space complexity would be : O(N)+O(N) or O(N). We can also use BFS traversal of graphs.

Java Code for BFS

import java.util.*;
public class Main{
    public static void main(String[] args){
         int n = 5;
        ArrayList < ArrayList < Integer >> graph = new ArrayList < ArrayList < Integer >> ();


        for (int i = 0; i < n+1; i++)
            graph.add(new ArrayList < Integer > ());


        graph.get(1).add(2);
        graph.get(2).add(1);


        graph.get(2).add(3);
        graph.get(3).add(2);


        graph.get(3).add(4);
        graph.get(4).add(3);


        graph.get(4).add(5);
        graph.get(5).add(4);
        
        graph.get(5).add(1);
        graph.get(1).add(5);


        System.out.println(isBipartite(graph,n));
    }
    
    public static boolean isBipartite(ArrayList<ArrayList<Integer>> graph,int n){
        
        int[] color=new int[n+1];
        Arrays.fill(color,-1);
        for(int i=1;i<=n;i++){
            if(color[i]==-1){
                if(bfs(graph,color,i)==false)
                return false;
            }
        }
        return true;
    }
    public static boolean bfs(ArrayList<ArrayList<Integer>> graph,int[] color,int node){
        
       Queue<Integer> q = new ArrayDeque<>();
       q.add(node);
       color[node]=0;
       while(q.size()>0){
           int top=q.poll();
           for(int nbr:graph.get(top)){
               if(color[nbr]==-1){
                   color[nbr]=1-color[top];
                   q.add(nbr);
               }else if(color[nbr]==color[top])
               {
                   return false;
               }
           }
       }
       return true;
    }
}

Time complexity

Here, we are traversing all over the graph so that it would be O(N+E).

Space complexity

O(N) for queue using and  O(N) for color array. If we ignore the space required to store the graph, then space complexity would be: O(N)