Biconnectivity in a Graph

What is a Graph?

A graph is a structure where values are stored at the vertex, and the relation between vertices is denoted by edges.

In a graph, if there is only one component, it is said to be a connected graph. So, a biconnected graph means a graph where there does not exist any articulation point.

What is an Articulation point?

If a graph contains an vertex that after removing that vertex, if the graph is divided into two or more components, then this vertex is called articulation point. For any articulation point, there will be the removal of that vertex and all its edges connected to it.

For getting an articulation point, the brute-force approach is by removing each vertex and checking if the graph is connected or not. If connected, then add it again and move to the next vertex. If not connected, then return true for articulation point.

For example:

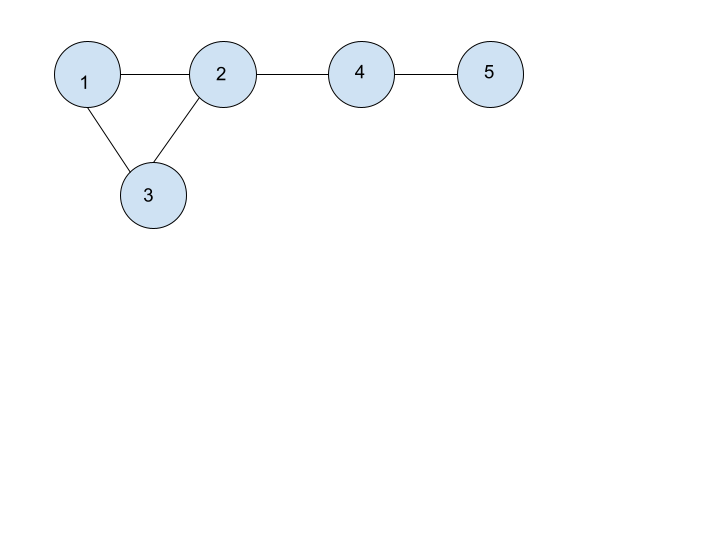
In the above graph, vertex 2 and vertex 4 are articulation points because if you remove any of them, the graph will be divided into two parts, and it will not be connected.

After removing vertex2:

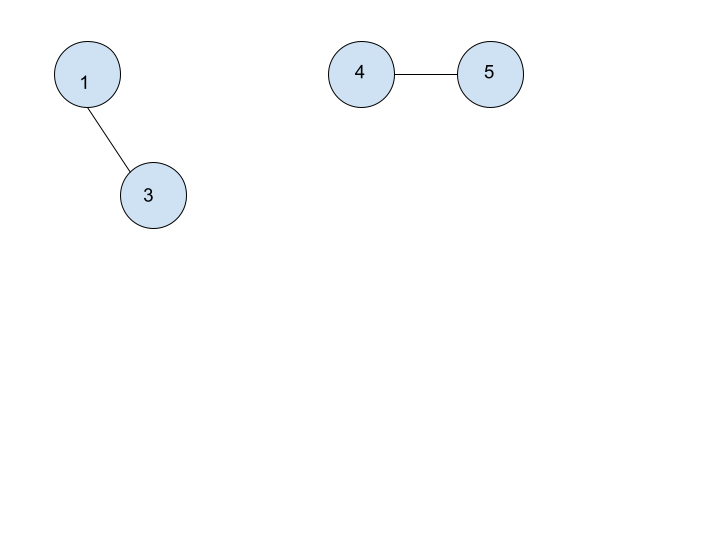
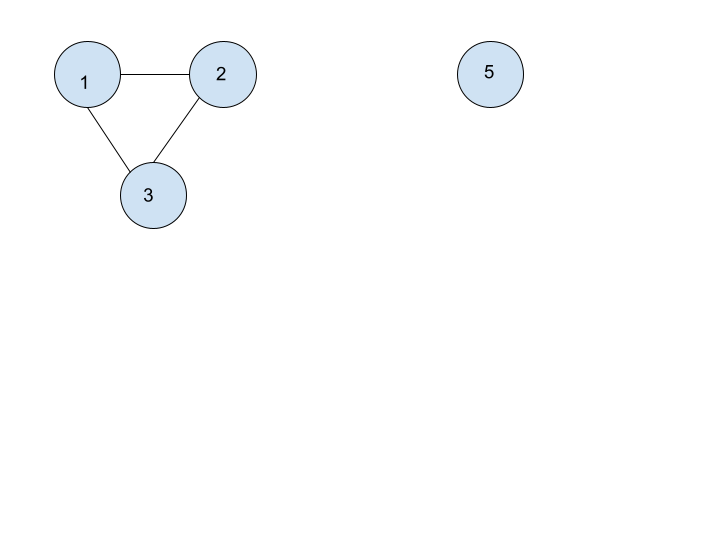
After removing 4:

If we try the brute-force approach, then it will not be an optimal solution. Let's suppose the number of vertices is V and edges is E. so, Time complexity would be: O(V*(V+E)).

For an optimal solution, we will use the DFS approach. The basic idea would be that during DFS, we will assign two variables for each node. The first one is the time for the node to be introduced, and the second one is the minimum to get to the node.

Initially, we will use the timer variable and assign them the same as the time and increment time variable.

During dfs, if the node is unvisited, make it visited.

Visit its adjacent node except the parent.

If the adjacent node is not visited, then call the recursive DFS function for this adjacent node.

When the adjacent node of any node is visited, then compare its minimum time to the node’s minimum time.

If (min_time[adjacent]>=min_time[node]), it means if we remove the current node, then we can't reach the adjacent node because the adjacent node’s path is dependent on the current node. So the current node is an articulation point for this adjacent node.

Else we can simply put min_time[node] = min_time[adjacent] because it shows adjacent node’s minimum time to reach is lesser than current. It means we can reach the adjacent node also without the current node. So the current node can’t be an articulation point.

Note: if there is any source vertex from where we are starting the DFS, and it has more than one child who is not connected, then it can be an articulation point

For example:

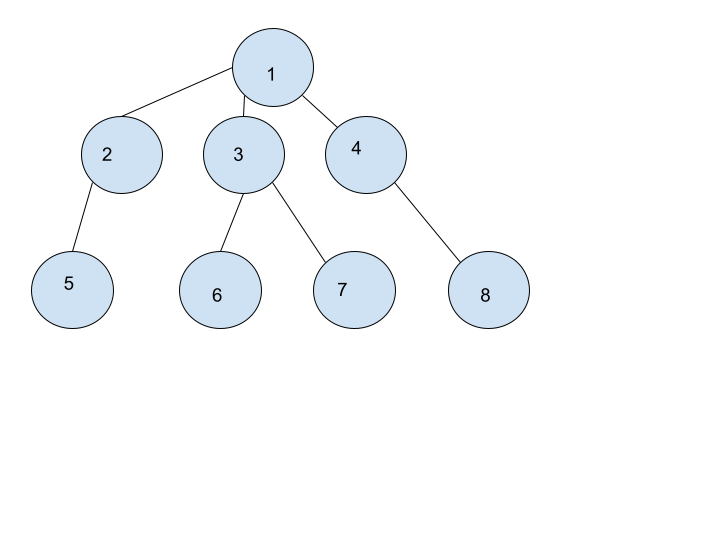
For the above, if we remove node 1, then it will be divided into more than one component.

So if there is any node whose parent is no node and it has more than one child, then it will definitely be an articulation point.

For implementing the code, we use a HashSet. If we encounter any articulation point, then we will add it to the HashSet.

In the end, if the HashSet contains more than zero elements, then the graph is not biconnected, else the graph is considered to be connected.

JAVA Code:

import java.util.*;
public class Main {
  public static void dfs(int node, int parent, int vis[], int tin[], int low[], ArrayList < ArrayList < Integer >> adj, int timer, HashSet < Integer > articulation) {
    vis[node] = 1;
    tin[node] = low[node] = timer++;
    int child = 0;
    for (Integer it: adj.get(node)) {
      if (it == parent) continue;


      if (vis[it] == 0) {
        dfs(it, node, vis, tin, low, adj, timer, articulation);
        low[node] = Math.min(low[node], low[it]);


        if (low[it] >= tin[node] && parent != -1) {
          articulation.add(node);
        }
        child++;
      } else {
        low[node] = Math.min(low[node], tin[it]);
      }
    }
    if (parent != -1 && child > 1) articulation.add(node);
  }


  public static void printBridges(ArrayList < ArrayList < Integer >> adj, int n) {
    int vis[] = new int[n + 1];
    int tin[] = new int[n + 1];
    int low[] = new int[n + 1];


    HashSet < Integer > articulation = new HashSet < > ();


    int timer = 0;
    for (int i = 0; i < n; i++) {
      if (vis[i] == 0) {
        dfs(i, -1, vis, tin, low, adj, timer, articulation);
      }
    }


    if (articulation.size() > 0)
      System.out.println("not biconnected");
    else
      System.out.println("bi-connected graph");
  }
  public static void main(String[] args) {
    int n = 5;
    ArrayList < ArrayList < Integer > > adj = new ArrayList < ArrayList < Integer > > ();
    for (int i = 0; i < n + 1; i++)
      adj.add(new ArrayList < Integer > ());


    adj.get(1).add(2);
    adj.get(2).add(1);


    adj.get(2).add(3);
    adj.get(3).add(2);


    adj.get(1).add(3);
    adj.get(3).add(1);


    adj.get(2).add(4);
    adj.get(4).add(2);


    adj.get(4).add(5);
    adj.get(5).add(4);


    printBridges(adj, n);
  }
}

So the time complexity for the above code is O(V+E) as we are doing normal DFS traversal.