IEEE Standard 754 Floating Point Numbers

Floating Point Representation: IEEE- 754

There were many problems in the conventional representation of floating-point notation like we could not express 0(zero), infinity number. To solve this, scientists have given a standard representation and named it as IEEE  Floating point representation.

IEEE stands for “ The Institute of Electrical and Electronics Engineers." It's an association that develops, defines and reviews the standard of electrical and computer science engineering. IEEE in 1985 and augmented in 2008 provided a standard to represent floating-point numbers and process them. This standard is now used by all the manufacturers while designing the floating-point arithmetic units to be portable among computers.

History of IEEE Floating Point Standard 754 -1985 & innovation in 2008

In the mid-'50s, floating-point binary numbers were used in the beginning without a format. As there was no defined format to represent floating-point numbers in computers, creating problems in the portability of programs from one manufacturer's computer to another manufacturer's computer. With the innovation of personal computers in the mid-1980s, the number of bits used to store floating-point numbers was standardized as 32 bits. After that, a standing committee was formed by IEEE to standardize how floating-point binary numbers would be represented in computer and to resolve exception conditions such as an attempt to divide by 0, representation of infinity,0 and uniformity in rounding numbers.

Now, the system was able to use standard floating-point formats in 32 bits and 64 bits. With the innovation in computer technology, it became feasible to use many bits for floating-point numbers. IEEE 754 standard was updated in 2008 with a new standard for 16 bits and 128 bits numbers. The new version IEEE 754-2008 stated the standard for representing decimal floating-point numbers.

IEEE 754 standard has given the representation for floating-point number, i.e., it defines number representation and operation for floating-point arithmetic in two ways:-

1. Single precision (32 bit)
2. Double precision ( 64 bit )

 Single-Precision -

1. Sign- In single precision, 1 bit is assigned for the sign (positive or negative).
2. Exponent- 8 bit is assigned for the range named exponent.
3. Mantissa- 23 bit is assigned for the precision ( it's for the fractional part)

Note:                                                                    

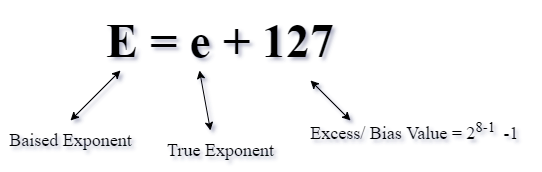
Why do we add 127?

Suppose a floating-point number:

                                1.1011 * 2⁺⁵           E = 5 + 127 = 132               positive

                                1.1011 * 2^-5           E = -5+ 127 = 122               number

To maintain the +ve exponent only, we have to add 127 & 1023 (due to this, exponent always remain positive). If we add number less than 127, then we attain – ve exponent.

Note:- (i) If a different sign for exponent is used while performing the floating-point arithmetic, the hardware only concentrates on the exponent sign to overcome certain hardware problems in the floating-point representation. The true component is added to 127 to manage the number in + ve form. End-user subtracts 127 when we give E' to end-user.

In double-precision (64- bit)

1. Sign- In single precision, 1 bit is assigned for the sign(positive or negative).
2. Exponent- 8 bit is assigned for the range named as an exponent.
3. Mantissa- 23 bit is assigned for the precision ( it's for the fractional part)

                                                  Excess = 2^n-1- 1

In single precision                                                     In double precision

N= E = 8                                                                    N= E = 11

So, Excess = 2^8-1- 1 = 127                                        So, Excess = 2^11-1- 1 = 1023

What is the range of E & e?

E = 8 bit (in single precision format)

So, maximum value of a 8 bit number = 2⁸ – 1= 255

Minimum value of a 8 bit number = 0

     0? E ? 255 (because using 8 bits, total combination become = 2⁸ =256[0-255]

But in actual the value for normal number    1? E ? 254

Therefore, 0 & 255 are  reserved for special number.

Example:- Represent the following number in single precision and double precision.

• (-23.875)₁₀
• (.75)₁₀

Solution:- (-23.875)₁₀ =  -(10111.111)₂ =  -1.0111111 * 2⁺⁴

                                                                         Mantissa

In single precision

S= 1 ( because number is –ve)

E= e + 127 = 4 +127 =131 =(10000011)₂

M= 0111111

S= 1

E =10000011

M=0111111…..

     1 bit                                      8 bit                                     23 bit

In double precision

S= 1 ( because number is –ve)

E= e + 1023 = 4 +1023 =1027 =(10000000011)₂

M= 0111111

S= 1

E =10000000011

M=0111111…..

1. bit                                      11 bit                                     52 bit

Q) (.75)₁₀

Solution:- (.75)₁₀ =  -(.11)₂ =  1.1 * 2^-1

In single precision

S= 0 ( because number is +ve)

E= e + 127 = -1 +127 =126 =(01111110)₂

M= 10000….

S= 0

E =011111110

M=10000…….

     1 bit                                      8 bit                                     23 bit

In double precision

S= 0 ( because number is +ve)

E= e + 1023 = -1 +1023 =1022 =(11100011110)₂

M= 100000…..

S= 1

E =11100011110

M=100000…..

     1 bit                                      11 bit                                     52 bit

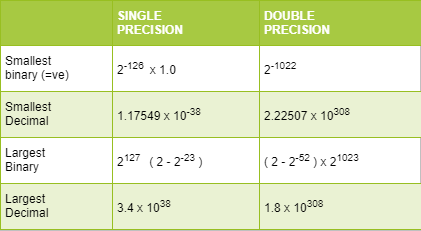
The maximum value in single precision

As we want maximum value so the number should be positive, i.e., S=0

      E _max= 254 = (11111110)₂

      M _max = 11111…….111(23 bit)

      V= (-1)⁵ (1.11111…..)₂  x 2^e         where e = E-127

      V= (-1)⁰ (1.11111…..)₂  x 2^254-127

  V=  (1.11111…..23 times)₂  x 2¹²⁷    

   V= ( 2⁰*1 + 1 * 2^-1 + 1 * 2^-2+………..1 * 2^-23) x 2¹²⁷

   V= ( 1+ ½ + ½^{2 +}½³………..½²³ ) x 2¹²⁷   

               G.P series with r = ½, a =1, n =24[0-23]

Sum of G.P Series = a(1-rⁿ) / 1-r = 2 x[1-2^-24]

V= 2 x(1-2^-24) x 2¹²⁷

    = (2-2^-23) x 2¹²⁷ = 3.4 x 10³⁸

Minimum value in single precision

As we want maximum value so the number should be negative i.e. S=1

      E _min= 254 = (11111110)₂

      M _min = 11111…….23 times(23 bit)

      V= (-1)⁵ (1.11111…..)₂  x 2^e         where e = E-127

         Answer  = -3.4 x 10³⁸

Maximum and Minimum value in Single and double precision

IEEE -784 Floating-Point Standard –New Version (2008)

IEEE 754 standard was updated in 2008 with a new standard for 16 bits and 128 bits numbers. These are made to solve exact decimal computation required in financial transactions and for working in the graphic area, and using high-performance computers for intensive numeric computation.

16-bit Standard Representation  

Sign	Exponent	Significant
I bit	5 bits	10 bits

The maximum positive integer is

+ 1.111..1 × 2 ¹⁵

 = 1 + (1 – 2^{– 11})×2 ¹⁵

 = (2 – 2^–11)×2 ¹⁵

  ? 65504.

The minimum positive number is

+ 1.000 … 0 × 2 ^–14

= 2 ^–14

= 0.61 × 10^-4 .

128-bit Standard Representation 

Sign	Exponent	Significant
I bit	14 bits	113 bits

The largest positive number which can be represented in this format is

(1 – 2^–113)×2¹⁶³⁸³

 ? 10⁴⁹³².

The smallest normalized positive number is:-

 = 2 ^1–16383

= 2 ^–16382

 ? 10 ^–4931 .