Computer Organization and Architecture Data Formats

Data Formats

In the digital world, everything is based on digits. In every method, the calculation is processed on the digits, and most importantly, the computer only understands the binary language (digits 0 & 1). These digits are input Data for the system to fetch, process and execute the instruction.

Data is the raw information or collection of instruction provided to the system to execute that instruction to gain a required output. So it becomes necessary to enter that data in a particular format according to the system's requirement, which is called data formatting.

Data Format – Data format is nothing but the exact way of representing data in Binary. It tells how, why and which data format is suitable for executing that particular system's particular task. Various kinds of data are entered in the system; data format provides the user criteria to systematically use that data.

Why are data formats necessary to understand in Computer Organization and Architecture?

In Computer Organization and Architecture, data formats are necessary to understand in architecture. During designing, the CPU user needs to decide that the CPU will take Number (data)  in which format. Some criteria are already set in the system for the working of the processor. For example, if a system understands the Number in 1's complement number representation and provides CPU data in 2's complement number representation, the CPU gives you an incorrect answer. 

In system architecture, the designer already set a word size like a word size of 16 bit or 32 bit or 62 bit. If the user system is 32 bit and the user is installing an application of 64-bit configuration, that application doesn't work properly. The application always shows a problem in the running of the system.     

Types of Data input in Computer

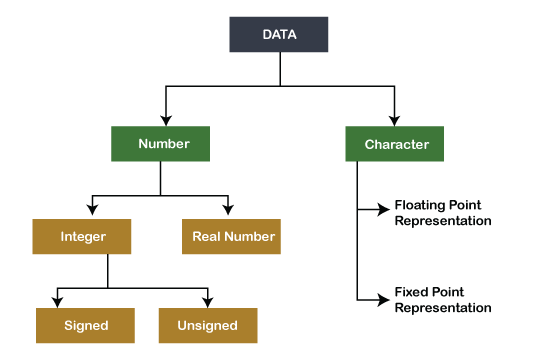
Number

Numbers are digits (0-9) used for calculating (subtraction, addition, multiplication, division and other mathematical calculation). Mathematics is originated with numbers. In a computer system, numbers are represented in different ways.

Ways of number representation are:-

• Integer
• Real Number

Integer

Integers are the whole Number (not a fraction) represented in the computer as a group of binary digits (bits). These are some of the data types commonly used in computers. Integers can be positive, negative or zero-like 34, -567  or 0, 45563.

Different integers are divided into two parts.

 

Unsigned type of integer

An unsigned integer can hold a whole number (0-n). Number (0-n) can be zero and positive Number like 0, 36277. Unsigned integers cannot use negative values or numbers.

If the computer has an 8-bit register to store Number, the range of unsigned integer is:-

• Smallest Number  = 0000000 =0
• Largest Number  = 1111111 = 2⁸ -1= 255

If the computer has a 16-bit register to store Number, the range of unsigned integer is:-

• Smallest Number = 000000000000000 =0
• Largest Number = 111111111111111 = 2¹⁶ -1= 65535

If the computer has a 32-bit register to store Number, the range of unsigned integer is:-

• Smallest Number =0
• Largest Number  = 2³² -1= 4,294,967,295 or about 4 billion.

 

Signed Integer

Like unsigned integer, signed integer also represents zero (0), positive value, but it can also represent Negative Number (-234). It is representing real Numbers as fixed-point representation in the system and will discuss further in detail.  In a computer system, there are three ways to represent signed integer:-

1. SMR- Sign Magnitude Representation.
2. 1's Complement Representation.
3. 2's Complement representation.

Here, the MSB (Most significant bit) and LSB (least significant bit) are used.

MSB (Most significant bit)- The leftmost and higher-order bit in the binary Number have a higher number. For example, in binary number 1001, the MSB is 1, and in binary number 0011, the MSB is 0.

• If MSB is 0, then the Number evaluated is positive.
• If MSB is one, then the Number evaluated is negative.

LSB (least significant bit) – Least significant bit is the smallest bit in the binary number series at the rightmost side. For example, in binary number 1010, the LSB is 0, and in binary number 0111, the LSB is 1.

The computer only understands binary numbers where 0 is for +ve (positive) and 1 for negative. In representation, 1 bit is reserved for the Number.

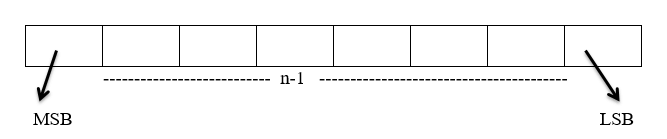
 Let, Total number of bits = n

Sign bit = 0 (it means number is positive)

Sign Bit = 1( It means Number is negative)

Important Point – For all positive signed integer numbers, all the three ways  (sign-magnitude, 1's complement, 2's complement)  have the same representation.

Representation of 25 in 8 bit using SMR, 1's complement and 2's complement.

0

0

0

1

1

0

0

1

Representation of -25 in 8-bit using SMR.

1

0

0

1

1

0

0

1

1's complement for negative Number

The working rule for finding 1's complement of negative Number.

Step 1: Represent the positive Binary of the given Number.

Step 2:  Inverse the digits (make 0 =>1 and 1 =>0). Hence we get 1’s compliment of that negative number. 

Representation of -45 (10101101) in 8 bit using 1's complement.

1

0

1

0

1

1

0

1

0

1

0

1

0

0

1

0

2's complement for negative Number

The working rule for finding 2's complement of negative Number.

Step 1: Find the Binary of positive Numbers.

Step 2: Scan that binary number from right to left , when 1 appears first then write the 1 as it is and inverse rest of the remaining digits . For example :-

Characters

Characters are words(letters, alphabet ) that we input in the system, but we cannot represent characters directly on a computer as we do with binary numbers. So to solve this, Scientists have given some different methods in Binary to represent the characters.

Method of representing a character in Binary called ALPHA NUMERIC CODES  and following are some codes:-

• MORSE CODE- It is the first alphanumeric code invented by FB morse. This symbol is used to represent some tasks.
•  

Symbol	Representation
.	Presence of current
-	Absence of current
A	.
5	…..
Apply	ATC and Telegraphy

• Morse code uses. (dot) and –(dashes) to represent letters and numbers.
• For example – A ->  .(dot) (.(dot) is followed by -)

                      Digit 5 -> …..( represented by 5 dots)

Morse code's main disadvantage was that it was variable-length code and can't be adopted by automated circuits like computers. It was used in applications like Telegraphy and Air traffic Control. It uses a combination of short (.) and long (-) elements.

• Barcode Code – It was similar to Morse code, but the only difference was that it uses 5-unit code that is unlike Morse code. It is fixed length Morse code. Here, alphabets are also represented. (dot) and –(dash).
• Holarith code -  It is a fixed-length code that uses a 12-bit representation of every alphabet.
• ASCII – Most of us are aware of this because it is currently used in Binary to represent the character. The full form of ASCII is the American Standard Code for information interchange. It is a method used to define a set of characters in the system. It is a seven-bit character code where every bit represents a unique character and can represent 128 different symbols.        
•                                   7 bit = 0000000 to 1111111

                                   0    to  2⁷ -1

• to  127

ASCII codes are used in computers, telecommunication equipment and other devices to represent the text. Uppercase letters and lower case letters are assigned different Numbers in the ASCII table. For example, character “B” is assigned to the decimal number “66” or  “0(zero)" is assigned to decimal number 48. Here's is an ASCII table with a symbol.

ASCII	Symbol	ASCII	Symbol	ASCII	Symbol	ASCII	Symbol
64	@	73	I	97	A	48	0
65	A	74	J	98	B	49	1
66	B	75	K	99	C	50	2
67	C	76	L	100	D	58	:
68	D	77	M	101	E	59	;
69	E	78	N	102	F	60	<
70	F	79	O	103	G	61	=
71	G	80	P	104	H	62	>
72	H	81	Q	105	I	63	?

• EBCDIC – EBCDIC stands for Extended Binary coded decimal interchange, which uses 8-bit binary code (a string of 0's or 1's) for each Number and alphanumeric character, including punctuation marks, accented letters and non-alphabetic characters. It is one of the data-encoding system designed and developed by IBM in which 256 possible characters are defined.  

• UNICODE – Unicode refers to the universal code. ISO designs the advanced and latest character encoding standard to support characters from all languages worldwide. Unicode supports 2 or 4 byte for each character. There are many types of Unicode encodings, such as UTF-8 and UTF-16.  Estimated Range of Unicode  = 0 to 2^16-1 = 0 to 65535  symbols. Programming language like Java uses UNICODE.

Real Numbers

The computer system uses two approaches to store real numbers.

1. Fixed point notation
2. ii) Floating-point notation.

Fixed point notation has fixed numbers after the decimal. For example, 364.432.

Floating-point allows varying numbers of digits after the decimal. For example 36.4423 x 10¹ or 3.64423 x 10². Digits are changing after the decimal. It will be discussed further in detail.