Conflict Serializability in DBMS

Conflict Serializability

A schedule is said to be conflict serializable if it can transform into a serial schedule after swapping of non-conflicting operations. It is a type of serializability that can be used to check whether the non-serial schedule is conflict serializable or not.

Conflicting operations

The two operations are called conflicting operations, if all the following three conditions are satisfied:

• Both the operation belongs to separate transactions.
• Both works on the same data item.
• At least one of them contains one write operation.

Note: Conflict pairs for the same data item are:
Read-Write
Write-Write
Write-Read

Conflict Equivalent Schedule

Two schedules are called as a conflict equivalent schedule if one schedule can be transformed into another schedule by swapping non-conflicting operations.

Example of conflict serializability:

Schedule S2 (Non-Serial Schedule):

Time	Transaction T1	Transaction T2	Transaction T3
t1	Read(X)
t2			Read(Y)
t3			Read(X)
t4		Read(Y)
t5		Read(Z)
t6			Write(Y)
t7		Write(Z)
t8	Read(Z)
t9	Write(X)
t10	Write(Z)

Precedence graph for schedule S2:

In the above schedule, there are three transactions: T1, T2, and T3. So, the precedence graph contains three vertices.

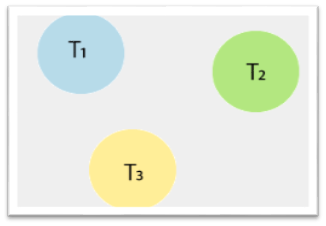
To draw the edges between these nodes or vertices, follow the below steps:

Step1: At time t1, there is no conflicting operation for read(X) of Transaction T1.
Step2: At time t2, there is no conflicting operation for read(Y) of Transaction T3.
Step3: At time t3, there exists a conflicting operation Write(X) in transaction T1 for read(X) of Transaction T3. So, draw an edge from T3?T1.

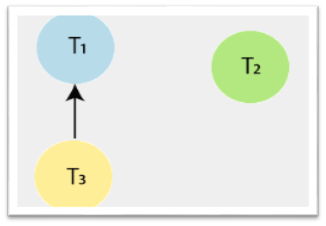
Step4: At time t4, there exists a conflicting operation Write(Y) in transaction T3 for read(Y) of Transaction T2. So, draw an edge from T2?T3.

Step5: At time t5, there exists a conflicting operation Write (Z) in transaction T1 for read (Z) of Transaction T2. So, draw an edge from T2?T1.

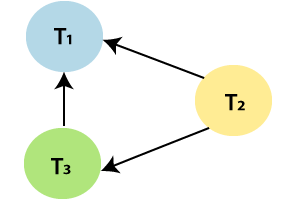
Step6: At time t6, there is no conflicting operation for Write(Y) of Transaction T3.
Step7: At time t7, there exists a conflicting operation Write (Z) in transaction T1 for Write (Z) of Transaction T2. So, draw an edge from T2?T1, but it is already drawn.

After all the steps, the precedence graph will be ready, and it does not contain any cycle or loop, so the above schedule S2 is conflict serializable. And it is equivalent to a serial schedule. Above schedule S2 is transformed into the serial schedule by using the following steps:

Step1: Check the vertex in the precedence graph where indegree=0. So, take the vertex T2 from the graph and remove it from the graph.

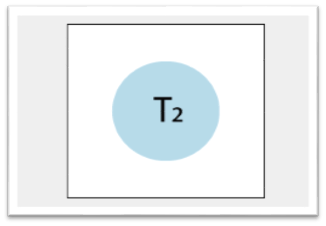
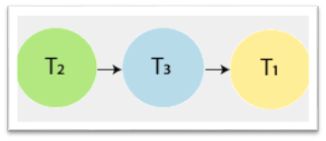
Step 2: Again check the vertex in the left precedence graph where indegree=0. So, take the vertex T3 from the graph and remove it from the graph. And draw the edge from T2?T3.

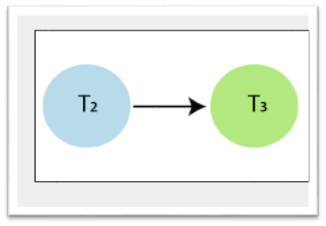
Step3: And at last, take the vertex T1 and connect with T3.

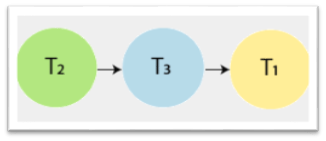
Precedence graph equivalent to schedule S2

Schedule S2 (Serial Schedule):

Time	Transaction T1	Transaction T2	Transaction T3
t1		Read(Y)
t2		Read(Z)
t3		Write(Z)
t4			Read(Y)
t5			Read(X)
t6			Write(Y)
t7	Read(X)
t8	Read(Z)
t9	Write(X)
t10	Write(Z)

Schedule S3 (Non-Serial Schedule):

Time	Transaction T1	Transaction T2
t1	Read(X)
t2		Read(X)
t3		Read (Y)
t4		Write(Y)
t5	Read(Y)
t6	Write(X)

To convert this schedule into a serial schedule, swap the non- conflicting operations of T1 and T2.

Time	Transaction T1	Transaction T2
t1		Read(X)
t2		Read (Y)
t3		Write(Y)
t4	Read(X)
t5	Read(Y)
t6	Write(X)

Then, finally get a serial schedule after swapping all the non-conflicting operations, so this schedule is conflict serializable.