Red-Black Tree Visualization in DBMS

Introduction to Red Black Tree

A red-black tree is a self-balanced binary search tree with an extra bit per node, usually read as a color (red or black). The tree is balanced with these colors during insertions and deletions. Although not perfectly balanced, the tree is good enough to reduce search time and bring the value closer to O (log n), in which n represents a wide variety of tree members. This tree was invented by Rudolf Bayer in 1972.

Note that these trees have the same memory footprint as traditional (non-colored) binary search trees. This is because each node only needs 1 bit of memory to store the color information.

 The tree is balanced using red and black colors. Due to node color constraints, simple root-to-leaf paths can be twice the length of other such paths. Red-black trees retain the ability to self-balance.

• The root of a red-black tree must always be black.
• There can never be two adjacent red nodes in a red-black tree.
• Each node must either be red or black (a red node cannot have a red parent node or a red child node). The number of black nodes on each path from a node (including the root) to any of its NULL nodes in its descendants is the same.
• There are only black leaf nodes.

Features of Red-Black Tree

• The color of the root node should always be black.
• Zero children of all nodes in a red-black tree are black.
• Descendants of red nodes are black. The black node could be the parent node of the red node.
• Each sheet has the same black depth.
• All direct connections from the root node to (downward) leaf nodes have the same number of black nodes.
• Tree roots are black.
• Whole leaves are black.
• Red nodes never have two consecutive red nodes because the descendants of red nodes are always black.
• The same black nodes appear in each straight path from a node to a descending leaf.

Visualization of Red-Black Tree

Visualization of Red-Black tree structures offers a simple representation of time and place.

The act or process of interpreting data into visual terms, such as images, graphs, or simulations, is known as visualization. An abstract or complicated concept can be communicated more clearly through visualization.

Tree analysis included multidimensional (3D) and continuous multilevel (CMP) spatial models of distributions. Both one-dimensional and multidimensional (NDS) analysis were performed along standard parameters during multispectral sampling (MSM). All analyses used the R package in the previous work to create visualization plans. An optional variable was added to each visualization plan included in the visualization algorithm as a result of the study data. The multilevel modeling model was developed to reflect that we have always used 3D models. All results are expressed as the mean squared error of the visualized data.

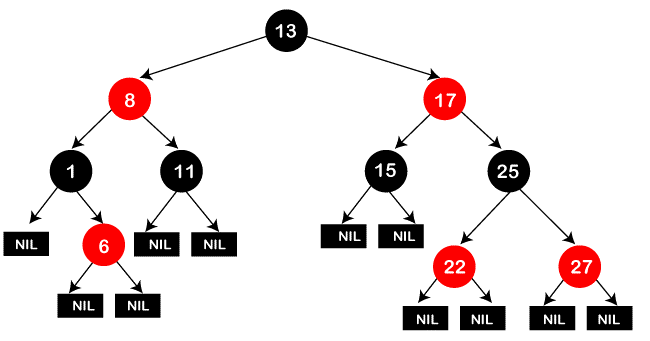
An element must be added using the following procedure to a red-black tree: 

1. Verify whether the tree is empty.
2. Add a new node as the root node in Black and complete the process if the tree is empty.
3. Paste the new node as a red leaf node if the tree is not empty.
4. If the new node's parent is Black, terminate the operation.
5. If the new node's parent is red, check the color of the new node's parent's siblings. 
6. Do the appropriate rotation and change the color for black or null nodes.
7. For red nodes, Recolor and Recheck. Repeat the same until the tree is a red-black tree.

To delete an element to a red-black tree, we have to follow the following algorithm:

1. First, find the item you want to remove.
2. Replace the node with the node holding the largest element in the left subtree if the element to be deleted is in a node with only the left children. (This node lacks the proper children.)
3. Replace the node with the node containing the smallest element in the right subtree if the element to be deleted is in a node with only the right children (this node has no left child).
4. If the element to be removed is in a node with left and right children, swap them in one of the two ways above. When replacing, replace only the value, not the color. 
5. The element to remove has exactly one left or right child. Replaces this node with its only child. 
6. This could violate the red constraint or the black constraint. Red constraint violations are easy to fix.
7. If the removed node is black, it violates the black constraint. If we remove the black node y, all paths containing y will have one less black node.
8. Next, it encounters two cases.
9. Replacement nodes are red. In this case, we color black to compensate for the loss of black nodes.
10. Exchange nodes are black.