Red-Black Tree Deletion in DBMS

Introduction To Red Black Tree

Each node's extra bit in a red-black tree, a type of self-balancing binary search tree, is frequently understood as the color (red or black). The balance of the tree is maintained through insertions and deletions, thanks to the employment of these colors. Although the tree's balance is not ideal, it is sufficient to cut down on searching time and keep it at or below O(log n), where n is the total number of tree elements. Rudolf Bayer invented this tree in 1972.

Note: It should be noted that these kinds of trees have the same memory footprints as the traditional (uncolored) binary search tree because each node only needs one bit of space to store the color information.

Requirement Of Red-Black Tree

Most BST operations, including search, max, min, insert, delete, and others, take O(h) time, where h is the BST's height. The cost of these procedures can go to O(n) for a skewed Binary tree. If we ensure that the tree's height remains O(log n) after each insertion and deletion, we may give an upper bound of O(log n) for all these operations. A Red-Black tree's height is always O(log n), where n is the tree's node count.

Properties of Red-Black Tree

• A self-balancing Binary Search tree is what it is. Self-balancing in this context indicates that it rotates or recolors the nodes to balance the tree.
• As each node in this tree data structure is either Red or Black, it is known as a Red-Black tree. Every node contains an additional piece of data known as a bit that corresponds to the node's color. For instance, 0 bits represent the color black, while 1 bit represents the node's red color. The node also stores data, left pointers, and right pointers, which are similar to the binary tree.
• The Red-Black tree's root node is always black.
• We refer to nodes in a binary tree with no children as leaves. On the other hand, the Red-Black tree's internal nodes are those without offspring; they are connected to the NIL nodes, which are consistently black in color. The Red-Black tree's leaf nodes are known as NIL nodes.
• Children of a Red node should be Black if the node is Red. In other words, there shouldn't be a red-red parent-child relationship.
• There should be an equal number of black nodes on any path leading from a node to any of its descendants' NIL nodes.

Deletion in Red Black Tree

Step 1:

First, we run the deletion using BST rules.

Step 2:

Case 1: If the node in question is Red and has to be eliminated, we just do that.

Consider removing node 31 from the tree, which is shown below.

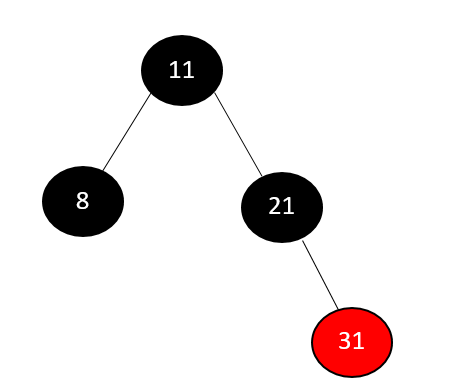
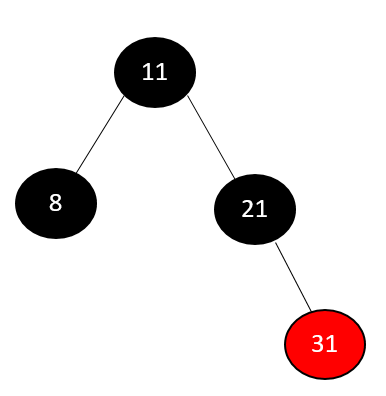
The root node's address is what we start with. We will first search the node using        BST. Given that 31 is greater than both 11 and 21, it follows that 31 belongs as a child of node 21. Node 31 is removed from the tree because it is a leaf node and is colored Red. Suppose the internal node with one child is to be deleted. Delete the child node after replacing the internal node's value with that of the child node.

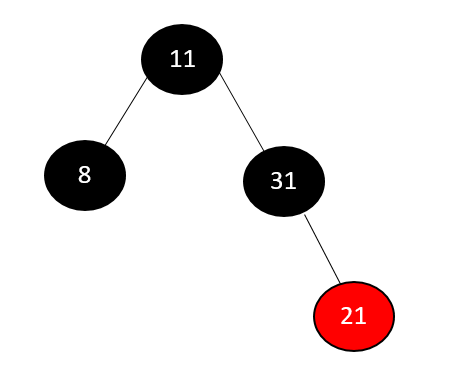
Take another instance where we wish to remove node 21, an internal node.

The internal node cannot be deleted; we can only change the value of that node to anything else. The single child of node 21, located to the right of the root node, is node 31. Therefore, node 21 is changed to have a value of 31, but the node's color, which is Black, stays the same.

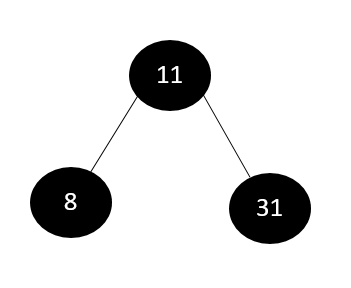
If the internal node with two child nodes has to be removed. In this situation, we must choose where to get the value for the internal node (either the left or right subtree). There are two options:

• In-order predecessor: The greatest value found in the left subtree will be substituted.
• In-order successor: The lowest value that is present in the correct subtree will be used as the successor in order.